The length of the chord of a circle is 8 cm and perpendicular distance between centre and the chord is 3 cm. Then the radius of the circle is equal to :
4 cm
5 cm
6 cm
8 cm
The correct Answer is:B
To find the radius of the circle given the length of the chord and the perpendicular distance from the center to the chord, we can follow these steps:
1. Identify the Given Information:
- Length of the chord (AB) = 8 cm
- Perpendicular distance from the center (O) to the chord (AB) = 3 cm
2. Divide the Chord:
- Since the perpendicular from the center to the chord bisects the chord, we can find the half-length of the chord.
- Half of the chord (AM) = AB/2 = 8 cm / 2 = 4 cm
3. Form a Right Triangle:
- We can form a right triangle using the radius (r), half of the chord (AM), and the perpendicular distance (OM).
- In triangle OMA:
- OM = 3 cm (perpendicular distance)
- AM = 4 cm (half of the chord)
- OA = r (radius of the circle)
4. Apply the Pythagorean Theorem:
- According to the Pythagorean theorem:
OA2=OM2+AM2
- Plugging in the values:
r2=32+42
r2=9+16
r2=25
5. Calculate the Radius:
- Taking the square root of both sides:
r=√25=5 cm
Final Answer:
The radius of the circle is 5 cm.
- Length of the chord (AB) = 8 cm
- Perpendicular distance from the center (O) to the chord (AB) = 3 cm
- Since the perpendicular from the center to the chord bisects the chord, we can find the half-length of the chord.
- Half of the chord (AM) = AB/2 = 8 cm / 2 = 4 cm
- We can form a right triangle using the radius (r), half of the chord (AM), and the perpendicular distance (OM).
- In triangle OMA:
- OM = 3 cm (perpendicular distance)
- AM = 4 cm (half of the chord)
- OA = r (radius of the circle)
- According to the Pythagorean theorem:
OA2=OM2+AM2
- Plugging in the values:
r2=32+42
r2=9+16
r2=25
- Taking the square root of both sides:
r=√25=5 cm
The radius of the circle is 5 cm.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)70videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)90videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XI)22videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
Knowledge Check
- Question 1 - Select One
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length is
A√5 cmB2√5 cmC2√7 cmD√7 cm - Question 2 - Select One
In a circle, there are two chords opposite to the centre of the circle. The length of one chord and the radius of the circle is 6 cm and 5 cm respectively, and the distance between both the chords is 7 cm. Find the length of the second chord.
Aa) 8 cmBb) 10 cmCc) 6 cmDd) 14 cm - Question 3 - Select One
Calculate the length (in cm) of the chord of the circle which is at the distance of the 12 cm from the centre and at the radius of the circle is 13 cm.
A10B12C13D15
Find the length of the chord of a circle of radius 13 cm, whose distance from the centre is 12 cm.
View SolutionThe radius of a circle is 10 cm and the perpendicular form the centre to a chord is 8cm. Find the length of the chord.
(ii) The radius of a circle is 10 cm. its one chord is 16 cm long. Find the perpendicular distance of this chord form the centre.
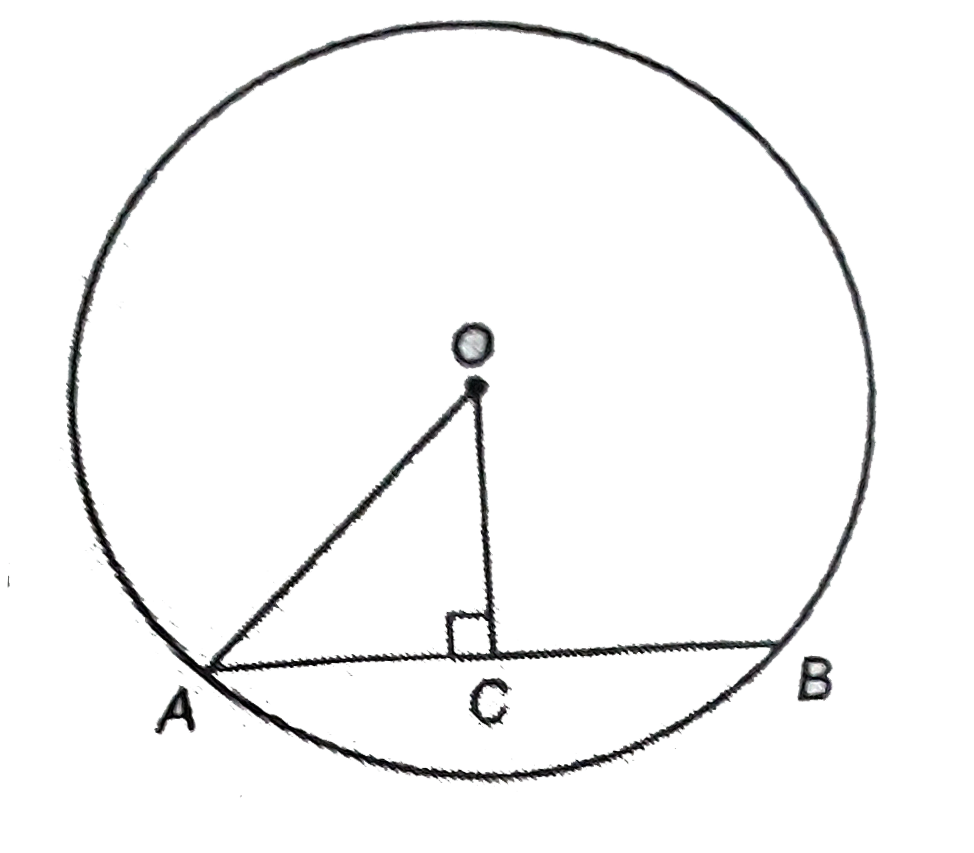
(iii) in the adjoining figure O is the centre of circle. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
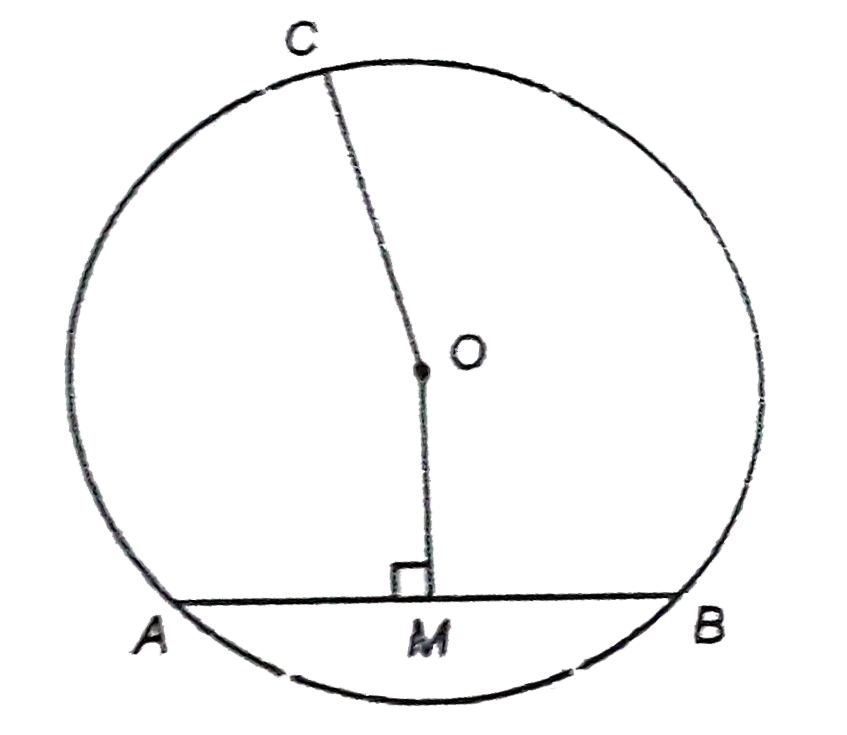
(iv) In the adjoining figure, OM⊥AB, radius OC=5cm and chord AB=8cm.Find the length of OM.
 View Solution
View SolutionFind the length of the chord of a circle whose radius is 7.5 cm, if its distance from the centre is 4.5 cm.
View SolutionTwo parallel chords are on one side of the centre of a circle. The length of the two chords is 24 cm and 32 cm. If the distance between the two chords is 8 cm, then what is the area (in cm2) of the circle?
View SolutionTwo parallel chords are on one side of the centre of a circle. The length of the two chords is 24 cm and 32 cm. If the distance between the two chords is 8 cm, then what is the area (in cm2) of the circle?
View Solution

