In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
2AB
√2AB
12AB
1√2AB
The correct Answer is:D
To find the length of the chord AC in a circle with center O, where AB and CD are two diameters that are perpendicular to each other, we can follow these steps:
1. Understanding the Circle and Diameters:
- We have a circle with center O.
- AB and CD are two diameters that intersect at O and are perpendicular to each other.
2. Label the Points:
- Let A, B, C, and D be points on the circle such that:
- A and B are endpoints of diameter AB.
- C and D are endpoints of diameter CD.
- The points A, C, B, and D can be visualized on the coordinate plane. For simplicity, we can place:
- O at the origin (0, 0).
- A at (-R, 0) and B at (R, 0) (where R is the radius).
- C at (0, R) and D at (0, -R).
3. Finding Coordinates of Points A and C:
- The coordinates of point A are (-R, 0).
- The coordinates of point C are (0, R).
4. Using the Distance Formula:
- To find the length of chord AC, we can use the distance formula:
AC=√(x2−x1)2+(y2−y1)2
- Substituting the coordinates of A and C:
AC=√(0−(−R))2+(R−0)2
AC=√(R)2+(R)2
AC=√2R2
AC=R√2
5. Relating to Diameter AB:
- The diameter AB is given as 2R.
- We can express AC in terms of the diameter:
AC=1√2×2R
6. Final Answer:
- Therefore, the length of chord AC is:
AC=2R√2=R√2
Conclusion:
The length of chord AC is R√2, which can also be expressed as 2R√2.
- We have a circle with center O.
- AB and CD are two diameters that intersect at O and are perpendicular to each other.
- Let A, B, C, and D be points on the circle such that:
- A and B are endpoints of diameter AB.
- C and D are endpoints of diameter CD.
- The points A, C, B, and D can be visualized on the coordinate plane. For simplicity, we can place:
- O at the origin (0, 0).
- A at (-R, 0) and B at (R, 0) (where R is the radius).
- C at (0, R) and D at (0, -R).
- The coordinates of point A are (-R, 0).
- The coordinates of point C are (0, R).
- To find the length of chord AC, we can use the distance formula:
AC=√(x2−x1)2+(y2−y1)2
- Substituting the coordinates of A and C:
AC=√(0−(−R))2+(R−0)2
AC=√(R)2+(R)2
AC=√2R2
AC=R√2
- The diameter AB is given as 2R.
- We can express AC in terms of the diameter:
AC=1√2×2R
- Therefore, the length of chord AC is:
AC=2R√2=R√2
The length of chord AC is R√2, which can also be expressed as 2R√2.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)70videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)90videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XI)22videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
In a circle with centre O, AB is a chord and BC is a diameter. From centre O. perpendicular OD is drawn to chord AB. Prove that OD=12AC. .
View SolutionIf Figure - 4, AB and CD are two diameter of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IF OA = 7 cm, then find the area of the shaded region.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
A2 ABB√2 ABC12ABD1√2 AB - Question 2 - Select One
Chords AB and CD of a circle interest at E and are perpendicular to each other. Segments AE, EB and ED are of lengths 2 cm, 6 cm and 3 cm respectively. Then the length of the diameter the circle in cm is :
A√65B12√65C65D652
In figure , AB and CD are two diameters of a circle ( with centre O) perpendicular to each other and OD is the diameter of the smaller circle . If OA = 7 cm , find the area of the shaded region.
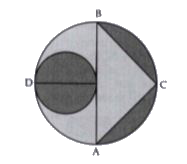 View Solution
View SolutionIn the given figure, AB and CD are two diameters of a circle (with centre 0) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
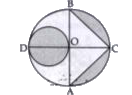 View Solution
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View SolutionIn Figure -4 AB, and CD are two diameters of a circle with centre O perpendiclualr to each other and OD is the diameter of the circle . If OA = 7 cm , then find the carea of the shaded region .
 View Solution
View SolutionAB and CD are two chords of circle with centre O and are perpendicular to each other. If ∠OAC=25∘ then ∠BCD = ?
View SolutionIn Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA=7 cm, find the area of the shaded region
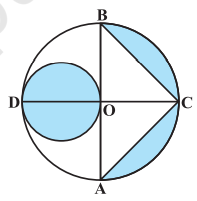 View Solution
View Solution

