Two equal circles intersect each other at points A and B, whose centres are O and O'. OO' = 24 mm and AB = 10 mm, then find the area (in sq. mm) of the circle.
530.66
520.66
510.33
500.33
The correct Answer is:A
To find the area of the circle given that two equal circles intersect at points A and B, with centers O and O', we can follow these steps:
Step 1: Understand the Geometry
The centers of the two circles, O and O', are 24 mm apart (OO' = 24 mm). The line segment AB, which connects the points of intersection of the circles, measures 10 mm.
Step 2: Determine the Midpoint
Since the circles are equal and intersect symmetrically, we can find the midpoint M of segment AB. This midpoint divides AB into two equal parts:
- AM = MB = 10 mm / 2 = 5 mm.
Step 3: Calculate Distances
The distance from the center O to the midpoint M (OM) can be found using the distance OO' and the properties of the right triangle formed by points O, M, and A.
- Since OO' = 24 mm, we can assume OM = 12 mm (half of OO').
Step 4: Use the Pythagorean Theorem
In triangle OAM, we can apply the Pythagorean theorem:
- OA² = OM² + AM².
Substituting the known values:
- OM = 12 mm,
- AM = 5 mm.
Calculating:
- OA² = 12² + 5²,
- OA² = 144 + 25,
- OA² = 169.
Step 5: Find the Radius
Now, take the square root to find OA (the radius of the circle):
- OA = √169 = 13 mm.
Step 6: Calculate the Area of the Circle
The area A of a circle is given by the formula:
- A = πr².
Using π ≈ 3.14 and r = 13 mm:
- A = 3.14 × (13)²,
- A = 3.14 × 169,
- A ≈ 530.66 mm².
Final Answer
The area of the circle is approximately 530.66 mm².
---
The centers of the two circles, O and O', are 24 mm apart (OO' = 24 mm). The line segment AB, which connects the points of intersection of the circles, measures 10 mm.
Since the circles are equal and intersect symmetrically, we can find the midpoint M of segment AB. This midpoint divides AB into two equal parts:
- AM = MB = 10 mm / 2 = 5 mm.
The distance from the center O to the midpoint M (OM) can be found using the distance OO' and the properties of the right triangle formed by points O, M, and A.
- Since OO' = 24 mm, we can assume OM = 12 mm (half of OO').
In triangle OAM, we can apply the Pythagorean theorem:
- OA² = OM² + AM².
- OM = 12 mm,
- AM = 5 mm.
- OA² = 12² + 5²,
- OA² = 144 + 25,
- OA² = 169.
Now, take the square root to find OA (the radius of the circle):
- OA = √169 = 13 mm.
The area A of a circle is given by the formula:
- A = πr².
- A = 3.14 × (13)²,
- A = 3.14 × 169,
- A ≈ 530.66 mm².
The area of the circle is approximately 530.66 mm².
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)70videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)90videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XI)22videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
If two equal circles whose centres are O and intersect each o ′ other at the point A and B, OO′ =12 cm and AB= 16 cm, then radius of the circle is:
यदि दो बराबर वृत्त जिनके केंद्र O तथा o ′ हैं, एक-दूसरे को बिंदु A तथा B पर काटते हैं, तथा OO′ =12 सेमी एवं AB = 16 सेमी है, तो वृत्त की त्रिज्या ज्ञात करें |View SolutionTwo equal circles intersect so that their centres, and the points at which they intersect form a square of side 1 cm. The area (in sq.cm) of the portion that is common to the circles is:
View Solution
Knowledge Check
- Question 1 - Select One
Two equal circles intersect each other at points A and B, whose centres are O and O'. OO' = 24 mm and AB = 10 mm, then find the area (in sq. mm) of the circle.
A530.66B520.66C510.33D500.33 - Question 2 - Select One
There are two circles intersecting each other . Another smaller circle with centre O , is lying between the common region of two larger circles. Centres of the circle ( i.e., A,O and B) are lying on a straight line. AB =16 cm and the radii of the larger circles are 10 cm each . What is the area of the smaller circle ?
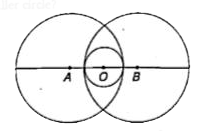 Aa. 4πcm2Bb. 2πcm2Ccc. 4πcm2Dd. π4cm2
Aa. 4πcm2Bb. 2πcm2Ccc. 4πcm2Dd. π4cm2
In the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point p within the circle. If AB=15cm,PB=9cm, then find the length of PD.
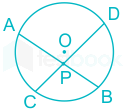 View Solution
View SolutionIf Figure - 4, AB and CD are two diameter of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IF OA = 7 cm, then find the area of the shaded region.
 View Solution
View SolutionIf the tangent at a point P to a circle with centre O cuts a line through O at Q such that PQ=24cm and OQ=25cm . Find the radius of the circle.
View SolutionIn the figure, two circles with centers O and P intersect each other at points D and C. Line AB intersects the circle with centre O at points A and B and touches the circle with centre P at point E. Prove ∠ADE+∠BCE=180∘.
 View Solution
View SolutionTwo equal circles intersect such that each passes through the centre of the other. If the length of the common chord of the circles is 10√3 cm, then what is the diameter of the circle?
View SolutionIn figure , AB and CD are two diameters of a circle ( with centre O) perpendicular to each other and OD is the diameter of the smaller circle . If OA = 7 cm , find the area of the shaded region.
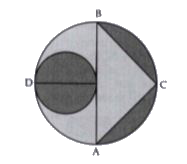 View Solution
View Solution

