In the given figure, B and C are the centres of the two circles. ADE is the common tangent to the two circles. If the ratio of the radius of both the circles is 3 : 5 and AC = 40, then what is the value of DE?
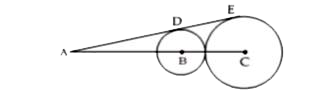
3√15
5√15
6√15
4√15
The correct Answer is:D
Step by step video, text & image solution for In the given figure, B and C are the centres of the two circles. ADE is the common tangent to the two circles. If the ratio of the radius of both the circles is 3 : 5 and AC = 40, then what is the value of DE? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
90 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
90 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
Knowledge Check
In the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
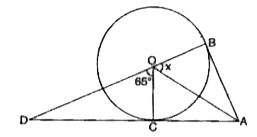 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘In the following figure, O is the centre of the circle. AB and CD are equal chords. If ∠AOB=100∘ , Find the ∠CED.
 AAC+AB=BCB3AE=AB+BC+ACCAB+BC+AC=4AED2AE=AB+BC+AC
AAC+AB=BCB3AE=AB+BC+ACCAB+BC+AC=4AED2AE=AB+BC+ACIn the given figure, the length of arc BC of the given circle is 44 cm. If O is the centre of circle, then what is the radius (In cm) of the circle ?
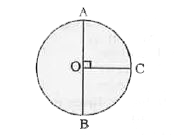 A7B14C28D35
A7B14C28D35
In given figure, O is the centre of the circle.
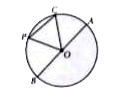
Which of the following is not the radius of the given circle?
View SolutionIn the given figure O is the centre of the circle and AB is a tangent at B. If AB=15 cm and AC=7.5 cm, find the rdius of the circle.

View SolutionIn the given figure two circles touch each other at the point C. Prove that the common tangent at P and Q.
View SolutionThe length of a common internal tangent to two circles is 5 and a common external tangent is 15, then the product of the radii of the two circles is :
View SolutionIn the given figure. AB. AC and EF are tangents to a circle. If AC = 15 cm and DE = 3 cm. then the length of AE is:
View Solution
