Question

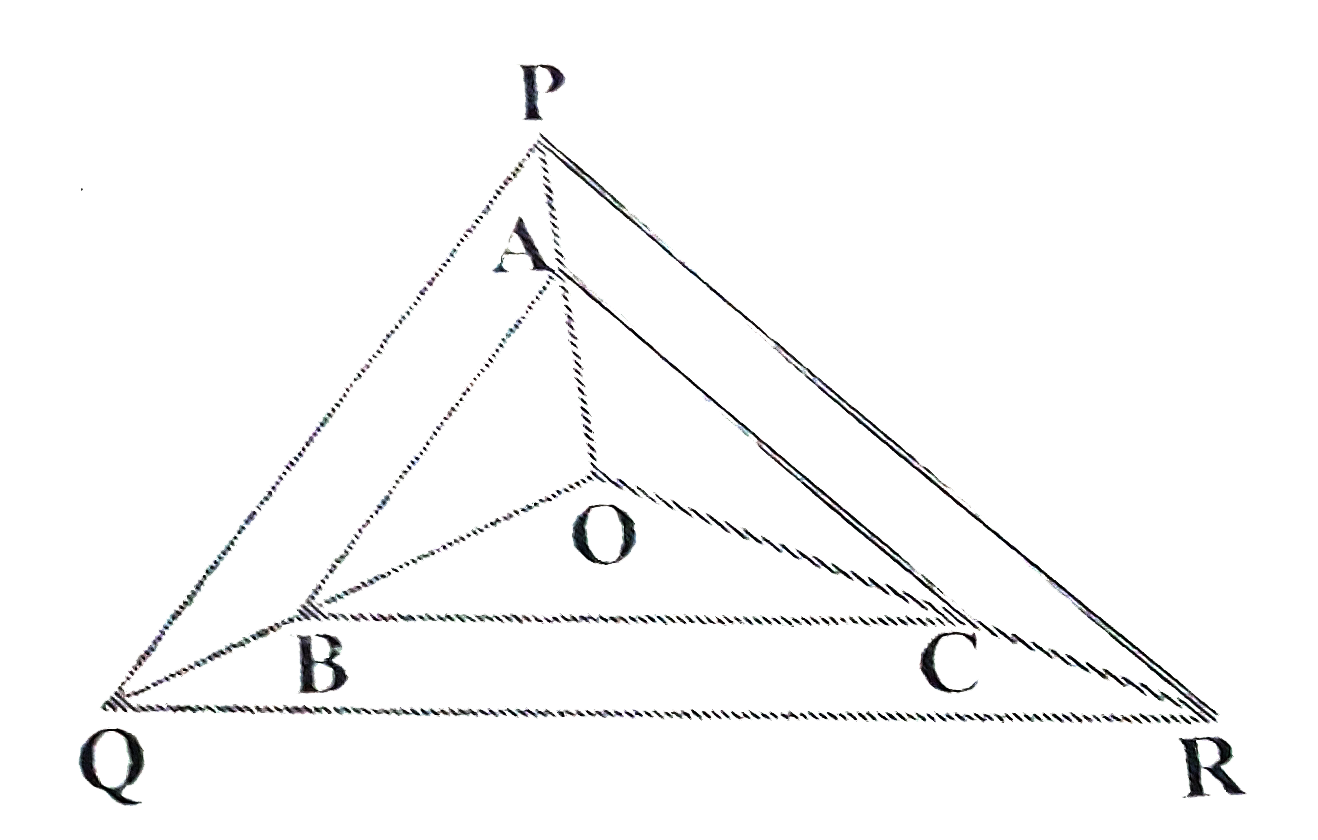
In triangle PQR, points A,B, and C are taken on PQ, PR and QR respectively such that $QC=AC$ and $CR=CB$ . If $\angle QPR={40}^{\circ }$ then $\angle ACB$ is equal to :

Options

A. `140^@`
B. `40^@`
C. `70^@`
D. `100^@`

Answer

D

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the Triangle and Given Information
We have triangle PQR with points A, B, and C on sides PQ, PR, and QR respectively. We know that:
- \( QC = AC \) (let's denote this length as \( x \))
- \( CR = CB \) (let's denote this length as \( y \))
- \( \angle QPR = 40^\circ \)

Step 2: Define Angles in Triangle QAC
In triangle QAC:
- Since \( QC = AC \), angles opposite these sides are equal. Thus, \( \angle CAQ = \angle AQC = x \).
- The angle at C, \( \angle ACQ \), can be calculated as:
\( \angle ACQ = 180^\circ - 2x \)

Step 3: Define Angles in Triangle BCR
In triangle BCR:
- Since \( CR = CB \), angles opposite these sides are equal. Thus, \( \angle CBR = \angle BRC = y \).
- The angle at C, \( \angle BCR \), can be calculated as:
\( \angle BCR = 180^\circ - 2y \)

Step 4: Use the Triangle Sum Property in Triangle PQR
In triangle PQR, the sum of the angles is:
\( \angle P + \angle Q + \angle R = 180^\circ \)
Given \( \angle P = 40^\circ \), we have:
\( 40^\circ + x + y = 180^\circ \)
This simplifies to:
\( x + y = 140^\circ \)

Step 5: Set Up the Equation for Angle ACB
Since \( ACB \) is a straight line, we have:
\( \angle ACB + \angle ACQ + \angle BCR = 180^\circ \)
Substituting the values we found:
\( \angle ACB + (180^\circ - 2x) + (180^\circ - 2y) = 180^\circ \)
This simplifies to:
\( \angle ACB + 360^\circ - 2x - 2y = 180^\circ \)
Rearranging gives:
\( \angle ACB = 180^\circ - 360^\circ + 2x + 2y \)
Substituting \( x + y = 140^\circ \):
\( \angle ACB = 180^\circ - 360^\circ + 2(140^\circ) \)
Calculating this gives:
\( \angle ACB = 180^\circ - 360^\circ + 280^\circ = 100^\circ \)

Final Answer
Thus, the measure of angle \( \angle ACB \) is \( 100^\circ \).

---