Derive an expression for the mutual induction of two long co-axial solenoids of same length would one over the other.
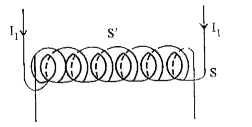
Consider the solenoids S and S. such that the solenoid S. completely surrounds the solenoid S.
Let length of each solenoid be l and the area of cross-seciton of each solenoid is A. Let N1 and N2 are the total number of turns of solenoid S and S. respectively.
∴ NO. of turns per unit length of solenoid S is given by, n1=N1l
No. of turn per unit length of solenoid S. is given by , n2=N2l
Let current I1 flow through solenoid S. Then magnetic filed inside the solenoid S is given by.
B1=μ0n1I1
=μ0N1I1l
∴ Magnetic flux linked with each turn of solenoid S. is given by dϕ2= BA
=μ0N1I1l1A
Then, total magnetic flux linked with N2 turns of the solenoid S. is given by
ϕ2=N2dϕ2
=μ0N1I1lA×N2
ϕ2=μ0N1N2I1Al ......(i)
But ϕ2=M12I1 .....(ii)
when M12 is the mutual inductance of coil S with respect to the coil S..
From (i) & (ii) , we get
M_(12) cancelI_(1) = (mu_(0)N_(1)N_(2) cancel(I_(1)) A)/(l)
M12=μ0N1N2Al .......(iii)
Now let current I2 flows through solenoid S. and no current through the solenoid S. The magnetic field inside solenoid S. is given by
B2=μ0n2I2=μ0(N2l)I2
Magentic flux linked with each turn of solenoid S,
dϕ1=B2A=μ0(N2l)I2A
∴ Total magnetic flux linked with each all turns of solenoid S
ϕ1=N1dϕ1=μ0(N1N2l)I2A .......(iii)
Also, ϕ=M21I2 ......(v)
where M21 is mutual induction of solenoid S. w.r.t. solenoid S
from eqn. (iv) and (v), we get
M_(12) cancel(I_(2)) = (mu_(0)N_(1)N_(2)A)/(l)cancel(I_(2))
M21=μ0N1N2Al .......(vi)
Comparing (iii) and (vi), we find
M12=M12M (say)
Thus M=μ0N1N2lA
M=μ0(N1l)(N2l)×Al
=μN1N2Al2=μ0N1lN2lAl
M=μ0n1n2Al
Similar Questions
(a) Define mutual inductance and write its SI units.
(b) Derive an expression for the mutual inductance of two long co-axial solenoids of same length wound one over the other.
(c) In an experiment, two coils C1andC2 are placed close to each other. Find out the expression for the emf induced in the coil C1 due to a change in the current through the coil C2.
View SolutionDefine mutual inductance between a pair of coils. Derive expression for the mutual inductance of two long coaxial solenoids of same length wound one over the other.
View SolutionWrite an expression for mutual inductance of two co-axial solenoids.
View SolutionDefine mutual inductance between two long coaxial solenoids. Find out the expression for the mutual inductance of inner solenoid of length l having the radius r1 and the number of turns n1 per unit length due to the second other solenoid of same length and n2 number of turns per unit length.
View SolutionDeduce an expression for the mutual inductance of two long coaxial solenoids but having different radii and different number of turns.
Or
Obtain the expression for the mutual inductance of two long coaxial solenoids S1 and S2 wound one over the other, each of length I and radii r1andr2, and number of turns per unit length n1andn2 respeetively, when a current I is set up in the outer solenoid S2.
View SolutionWrite an expression for self inductance of a long solenoid.
View SolutionDefine the term 'mutual inductance between the two coils. Obtain the expression for mutual inductance of a pair of long coaxial solenoids each of length l and radii r1andr2(r2>r1). Total number of turns in two solenoids are N1andN2 respectively.
View SolutionDerive the expression for the self inductance of a long solenoid of cross sectional area A and length l, having n turns per unit length.
View Solution(a) Define self inductance. Write its S.I. units
(b) Derive and expression for self inductance of a long solenoid of length l cross-sectional area A having N number of turns.
View SolutionDefine self-inductance. Write its SI unit. Derive an expression for self-inductance of a long, aircored solenoid of length l, cross-sectional area A (radius r), and having N number of turns.
View Solution
