An alternating e.m.f. is supplied to a pure resistance. Investigate the phase relationship between the current passing through it and e.m.f applied.

Text Solution

Verified by Experts

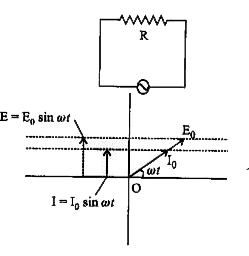
Let a source of alternating e.m.f. be connected to a pure resistance R. Suppose the alternatine e.m.f. supplied is represented by
$E = E_{0} sin ω t$ …(1)
Let I be the current in the circuit at any instant t According to ohm.s law, the potential difference developed across R will be IR. This must be equal to e.m.f. applied at the instant, i.e.,
$I R = E = E_{0} sin ω t$
or $I = \frac{E_{0}}{R} sin ω t = I_{0} sin ω t$ .....(2)
Where, $I_{0} = \frac{E_{0}}{R}$ , (maximum value of current)
Conclusion : From (1) & (2) in an a.c. circuit containing R only, the E and I are in the same phage.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Similar Questions

Knowledge Check

Question 1 - Select One
An alternating e.m.f. is applied to purely capacitive circuit. The phase relation between e.m.f. and current flowing in the circuit is or in a circuit containing capacitance only
Ae.m.f. is ahead of current by $π / 2$
BCurrent ahead of e.m.f by $π / 2$
CCurrent lags behind e.m.f. by $π$
DCurrent is ahead of e.m.f. by $π$
Question 2 - Select One
If an alternating e.m.f. is applied to a series L-R circuit, the phase angle between e.m.f. and current is given by $tan θ = \frac{ω L}{R}$ . Hence the power factor of the series L-R circuit is
A1. $\frac{ω L}{R}$
B2. $\frac{R}{ω L}$
C3. $\frac{R}{R + ω L}$
D4. $\frac{R}{\sqrt{R^{2} + ω^{2} L^{2}}}$
Question 3 - Select One
An alternating emf, e=300 sin100 $π t$ volt, is applied to a pure resistance of 100 $Ω$ . The rms current through the circuit is
A2.12 A
B0.212 A
C20.12 A
D0.0212 A

Recommended Questions

Home
Ask Doubt
Profile