The magnetic flux through a coil is perpendicular to its plane and directed into the paper is verying according to the relation $ϕ = (2 t^{3} - t^{2} - 3 t + 5) w b$ . Find the e.m.f. induced in the coil at t = 2 s.

Text Solution

Verified by Experts

$ϕ = 2 t^{3} - t^{2} 3 t + 5$
$e = \frac{d ϕ}{d t}$
$e = \frac{d}{d t} (2 t^{3} - t^{2} - 3 t + 5)$
$e = 6 t^{2} - 2 t - 3 + 0$
$t = 2 s$
$∴ e = 6 {(2)}^{2} - 2 (2) - 3$
$= 24 - 4 - 3$
= 24-7
e = 17 volt.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Similar Questions

Knowledge Check

Question 1 - Select One
The magnetic flux through a coil perpendicular to its plane and directed into paper is varying according to the relation $ϕ = (2 t^{2} + 4 t + 6) m W b$ . The emf induced in the loop at t=4 s is
A0.12 V
B2.4 V
C0.02 V
D1.2 V
Question 2 - Select One
The magnetic flux through a coil perpendicluar to its plane and directed into paper is varying according to the relation $ϕ = (2 t^{2} + 4 t + 6) m W b$ . The emf induced in the loop at t=4 s is
A0.12 V
B2.4 V
C0.02 V
D1.2 V
Question 3 - Select One
In the figure the flux through the loop perpendicular to the plane of the coil and direciton into the paper varying according to the relation $ϕ = 6 t^{2} + 7 t + I$ where $ϕ$ is in milliweber and $t$ is in loop at $t = 2 s$ and direction of induced current through $R$ are
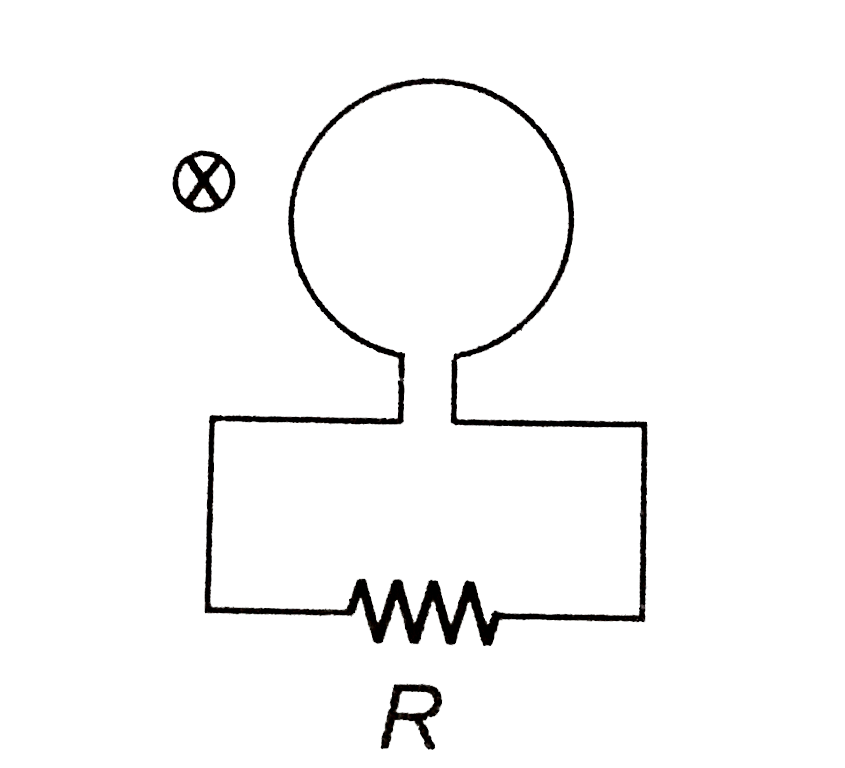A $39 m V$ , right to left
B $39 m V$ , left to right
C $31 m V$ right to left
D $31 m V$ , left to right

Recommended Questions

Home
Ask Doubt
Profile