If →a,→b,and→c are three non-coplanar non-zero vecrtors, then prove that (→a.→a)→b×→c+(→a.→b)→c×→a+(→a.→c)→a×→b=[→b→c→a]→a.Solution in Tamil
always lies in the plane containing →a+→b
always lies in the plane containing →a−→b
can be zero
cannot be zero
Step by step video & image solution for If vec a , vec b ,a n d vec c are three non-coplanar non-zero vecrtors, then prove that ( vec adot vec a) vec bxx vec c+( vec adot vec b) vec cxx vec a+( vec adot vec c) vec axx vec b=[ vec b vec c vec a] vec adot by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
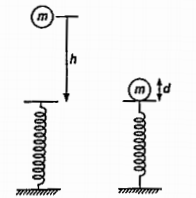
A vertical spring with force constant K is fixed on a table. A ball of mass m at a height H above the free upper end of the spring falls vertically on the spring so that the spring is compressed by a dsitance d. The net work done in the process is:
View Solutionlonization potential of hydrogen atom is 13.6 eV. Hydrogen atoms in the ground state are excited by monochromatic radiation of photon energy 12.1 eV. The spectral lines emitted by hydrogen atoms according to Bohr's theory will be
View SolutionThe vectors →a and →b are not perpendicular and →c and →d are two vectors satisfying : →b×→c=→b×→d,→a⋅→d=0 . Then the vector →d is equal to : (1) →b−⎛⎝→b.→c→a.→d⎞⎠→c (2) →c+⎛⎝→a.→c→a.→b⎞⎠→b (3) →b+⎛⎝→b.→c→a.→b⎞⎠→c (4) →c−⎛⎝→a.→c→a.→b⎞⎠→b
View SolutionIf →a,→band→c are three non coplanar vectors, then prove that →d=→a.→d[→a→b→c](→b×→c)+→b.→d[→a→b→c](→c×→a)+→⋅→d[→a→b→c](→a×→b)
View SolutionIf vectors →a,→b,and→c are coplanar, show that ∣∣∣→a→b→c→a.→a→a.→b→a.→c→b.→a→b.→b→b.→c∣∣∣=⊙
View SolutionIf →a.→b=→a.→c and →a×→b=→a×→c, →a≠0, then →b=→c b. →b=0 c. →b+→c=0 d. none of these
View SolutionGiven that →a.→b=→a.→c,→a×→b=→a×→cand→a is not a zero vector. Show that →b=→c.
View SolutionIf the vectors →a,→b,and→c form the sidesBC,CAandAB, respectively, of triangle ABC,then (a)→a.→b+→b.→c+→c.→a=0 (b)→a×→b=→b×→c=→c×→a (c). →a.→b=→b.→c=→c.→a (d). →a×→b+→b×→c+→c×→a=0
View SolutionIf →a is parallel to →b×→c , then (→a×→b).→a×→c is equal to |→a|2(→b.→c) b. ∣∣→b∣∣2(→a.→c) c. |→c|2(→a.→b) d. none of these
View SolutionIf →a, →b, →c are three vectors such that →a.→b=→a.→c then show that →a=0 or, →b=c or →a⊥(→b−→c).
View SolutionIf →a.→b=→a.→c and →a×→b=→a×→c, →a≠0, then
View SolutionIf a, b, c are non coplanar vectors then →a.→b×→c(→c×→a).→b+→b.→a×→c→⋅(→a×→b) is equal to 2 b. \ 0\ c. 1 d. none of these
View SolutionThe vectors →a and →b are not perpendicular and →c and →d are two vectors satisfying : →b×→c=→b×→d,→a⋅→d=0 . Then the vector →d is equal to : (1) →b−⎛⎝→b.→c→a.→d⎞⎠→c (2) →c+⎛⎝→a.→c→a.→b⎞⎠→b (3) →b+⎛⎝→b.→c→a.→b⎞⎠→c (4) →c−⎛⎝→a.→c→a.→b⎞⎠→b
View SolutionIf →a is perpendicular to →b and →r is non-zero vector such that p→r+(→r.→a)→b=→c, then →r= →cp−(→a.→c)→bp2 (b) →ap−(→⋅→b)→ap2 →ap−(→a.→b)→cp2 (d) →cp2−(→a.→c)→bp
View SolutionIf →a,→b,and→c are three non-coplanar non-zero vecrtors, then prove that (→a.→a)→b×→c+(→a.→b)→c×→a+(→a.→c)→a×→b=[→b→c→a]→a
View SolutionIf vec a , vec b ,a n d vec c are three non-coplanar non-zero vecrtors, then prove that ( vec a . vec a) vec bxx vec c+( vec a . vec b) vec cxx vec a+( vec a . vec c) vec axx vec b=[ vec b vec c vec a] vec a
View Solution
