Given the following statement :
If a quadrilateral is a parallelogram, then its diagonals bisect each other.
Identify these as contrapositive or converse of each other.Solution in Punjabi
The correct Answer is:True
Step by step video, text & image solution for Given the following statement : If a quadrilateral is a parallelogram, then its diagonals bisect each other. Identify these as contrapositive or converse of each other. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBOOK - SWAN PUBLICATIONCHAPTER - QUADRILATERALSEXERCISE - Objective Type Questions ( Fill in the Blanks)
10 Videos
- QUADRILATERALSBOOK - SWAN PUBLICATIONCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 8.2
7 Videos
- PROBABILITY BOOK - SWAN PUBLICATIONCHAPTER - PROBABILITY EXERCISE - OBJECTIVE TYPE QUESTIONS (FILL IN THE BLANKS)
6 Videos
- STATISTICS BOOK - SWAN PUBLICATIONCHAPTER - STATISTICS EXERCISE - Objective Type Questions (Fill in Blanks:)
1 Videos
Similar Questions
Sum of the angles of a quadrilateral is ................ .
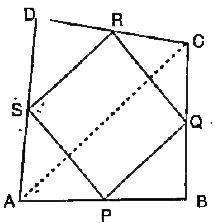
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that
SR∣∣AC and SR=12AC
(ii) PQ=SR
PQRS is a parallelogram.
View SolutionThe number of outcomes (m) favourable to an event cannot be ………………… than the total number of outcomes (n).
View SolutionThe mid value of the class intervals is known as the ...........
View SolutionState the converse and contrapositive of the following statement: If a quadrilateral is a parallelogram then its diagonals bisect each other.
View Solutionनीचे दिये (a) और (b) में दत्त कथनों में प्रत्येक के लिए संगत प्रतिधनात्मक और विलोम कथन पहचानिए :
(b) यदि एक चतुर्भुज समान्तर चतुर्भुज है, तो उसके विकर्ण एक-दूसरे को समद्विभाजित करते हैं :
(1) यदि एक चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं, तो चतुर्भुज एक समान्तर चतुर्भुज है।
(2) यदि एक चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित नहीं करते हैं, तो चतुर्भुज एक समान्तर चतुर्भुज नहीं है।
View SolutionProve, by vector method, that the diagonals of a parallelogram bisect each other , conversely, if the diagonals of a quadrilateral bisect each other, it is a parallelogram.
View SolutionGiven the following statements :
If a quadrilateral is a parallelogram, then its diagonals bisect each other.
Identify these as contrapositive or converse of each other.
View SolutionGiven the following statements :
A:If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
B: If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
Identify these as contrapositive or converse of each other.
View SolutionGiven the following statements :
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Identify these as contrapositive or converse of each other.
View SolutionGiven statements . Identify the statements given below as contrapositive or converse of each other.
If a quadrilateral is a parallelogram, then its diagonals bisect each other.
(i) If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
(ii) If the diagronals of a quadrilateral bisect each other, then it is a parallelogram.
View SolutionGiven statements in (a) and (b). Identify the statements given below as contrapositive or converse of each other.
(b) If a quadrilateral is a parallelogram, then its diagonals bisect each other.
(i) If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
(ii) If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
View SolutionGiven statements in (a) and (b). Identify the statements given below as contrapositive or converse of each other.
(b) If a quadrilateral is a parallelogram, then its diagonals bisect each other.
(i) If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
(ii) If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
View SolutionGiven statements in (a) and (b). Identify the statements given below as contrapositive or converse of each other.
(b) If a quadrilateral is a parallelogram, then its diagonals bisect each other.
(i) If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
(ii) If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
View SolutionGiven statements in (a) and (b). Identify the statements given below as contrapositive or converse of each other.
(b) If a quadrilateral is a parallelogram, then its diagonals bisect each other.
(i) If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
(ii) If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
View SolutionGiven statements in a and b. Identify the statements given below as contrapositive or converse of each other.
If a quadrilateral is a parallelogram, then its diagonals bisect each other.
(i) If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram
(ii) If the diagonals of the quadrilateral bisect each other then it is a parallelogram.
View Solution
