Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter(say d). That is, π=cd. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?Solution in Punjabi
Step by step video & image solution for Recall, pi is defined as the ratio of the circumference (say c) of a circle to its diameter(say d). That is, pi=c/d. This seems to contradict the fact that pi is irrational. How will you resolve this contradiction? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NUMBER SYSTEMSBOOK - SWAN PUBLICATIONCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.6
11 Videos
- NUMBER SYSTEMSBOOK - SWAN PUBLICATIONCHAPTER - NUMBER SYSTEMSEXERCISE - OBJECTIVE TYPE QUESTIONS
34 Videos
- NUMBER SYSTEMSBOOK - SWAN PUBLICATIONCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.4
1 Videos
- LINES AND ANGLES BOOK - SWAN PUBLICATIONCHAPTER - LINES AND ANGLES EXERCISE - Objective Type Questions (Solve the following questions)
2 Videos
- POLYNOMIALS BOOK - SWAN PUBLICATIONCHAPTER - POLYNOMIALS EXERCISE - OBJECTIVE TYPE QUESTIONS
23 Videos
Similar Questions
Find : 6412.
View SolutionState whether the statement are true (T) or false (F):
Any number which can be written in the form pq, where p and q are integers and q≠0 is called rational number.
View SolutionVisualise 3.765 on the number line, using successive magnification.
View SolutionIn Fig., find the value of x.
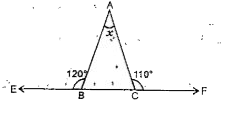
View SolutionState whether the statements are True (T) and False (F).
A polynomial having only one term is called monomial.
View SolutionRecall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π=cd. This seems to contradict the fact the πis irrational How will you resolve this contradiction?
View SolutionIf the circumference and the area of a circle are numerically equal, then diameter of the circle is (a) π2 (b) 2π (c) 2 (d) 4
View SolutionThe ratio of the perimeter (circumference) and diameter of a circle is π (b) 2π π2 (d) π4
View SolutionThe area of a circle of circumference C is (a)C24π (b) C22π (c)C2π (d) 4C2π
View SolutionIf the circumference and the area of a circle are numerically equal, then the diameter is equal to π2 (b) 2 π (c) 2 (d) 4
View Solutionπ को एक वृत्त की परिधि (मान लीजिए c) और उसके व्यास (मान लीजिए d) के अनुपात से परिभाषित किया जाता है, अर्थात π=cd है। यह इस तथ्य का अंतर्विरोध करता हुआ प्रतीत होता है कि π अपरिमेय है। इस अंतर्विरोध का निराकरण आप किस प्रकार करेंगे?
View SolutionReal π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d) i.e π=cd this seems to contradict the fact that π is irrational how will you resolve this contradication ?
View Solutionπ is the proportion of the cirumference (let c) of a circle to the diamter (let d) of it, i.e, π=cd where c and d are both terminting , then how is π an irrational number ? Explain.
View Solutionpi Recall that this is the ratio of the circumference (c) and diameter (d) of a circle. That is pi=c//d It is pi It seems to be the opposite of a rational number. How do you resolve this paradox?
View SolutionThe ratio of a circle to its diameter is c / d pi Referred to as, and pi Why is rational number considered on?
View SolutionRecall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π=cd. This seems to contradict the fact the πis irrational How will you resolve this contradiction?
View Solution
