Find the horizontal force and a force inclined at an angle of 60∘ with the vertical so that the resultant is a vertical force of P kg wt.
P, 2P
P, P√3
P√3,2P
none
The correct Answer is:C
To solve the problem of finding the horizontal force F1 and the force F2 inclined at an angle of 60∘ with the vertical such that the resultant force is a vertical force of P kg wt, we can follow these steps:
Step 1: Define the Forces
Let:
- F1 be the horizontal force.
- F2 be the force inclined at 60∘ with the vertical.
Step 2: Resolve F2 into Components
Since F2 is inclined at 60∘ with the vertical, we can resolve it into horizontal and vertical components:
- The vertical component of F2 is F2cos(60∘).
- The horizontal component of F2 is F2sin(60∘).
Step 3: Write the Equations for Resultant Forces
The resultant force in the vertical direction must equal P kg wt. Therefore, we can write:
F2cos(60∘)=P
And since the horizontal forces must balance out (as there is no resultant horizontal force), we have:
F1=F2sin(60∘)
Step 4: Substitute the Values of Cosine and Sine
Using the values:
- cos(60∘)=12
- sin(60∘)=√32
We can substitute these into our equations:
1. From the vertical force equation:
F2⋅12=P⟹F2=2P
2. From the horizontal force equation:
F1=F2⋅√32=2P⋅√32=√3P
Step 5: Final Answers
Thus, the horizontal force F1 and the inclined force F2 are:
- F1=√3P
- F2=2P
Summary of Results
- Horizontal Force F1=√3P
- Force Inclined F2=2P
Let:
- F1 be the horizontal force.
- F2 be the force inclined at 60∘ with the vertical.
Since F2 is inclined at 60∘ with the vertical, we can resolve it into horizontal and vertical components:
- The vertical component of F2 is F2cos(60∘).
- The horizontal component of F2 is F2sin(60∘).
The resultant force in the vertical direction must equal P kg wt. Therefore, we can write:
F2cos(60∘)=P
And since the horizontal forces must balance out (as there is no resultant horizontal force), we have:
F1=F2sin(60∘)
Using the values:
- cos(60∘)=12
- sin(60∘)=√32
1. From the vertical force equation:
F2⋅12=P⟹F2=2P
2. From the horizontal force equation:
F1=F2⋅√32=2P⋅√32=√3P
Thus, the horizontal force F1 and the inclined force F2 are:
- F1=√3P
- F2=2P
- Horizontal Force F1=√3P
- Force Inclined F2=2P
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - ADDITION AND MULTIPLICATION OF VECTORS EXERCISE - Problem Set (1) (TRUE AND FALSE )3videos
ADDITION AND MULTIPLICATION OF VECTORS
- BOOK - ML KHANNACHAPTER - ADDITION AND MULTIPLICATION OF VECTORS EXERCISE - Problem Set (1) (FILL IN THE BLANKS )3videos
ADDITION AND MULTIPLICATION OF VECTORS
- BOOK - ML KHANNACHAPTER - AREA OF CURVESEXERCISE - SELF ASSESSEMENT TEST16videos
AREA OF CURVES
Similar Questions
Knowledge Check
- Question 1 - Select One
A block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is
 AP+Qsinθmg+QcosθBPcosθ+Omg−QsinθCP+Qcosθmg+QsinθDΨnθ−Qmg−Qcosθ
AP+Qsinθmg+QcosθBPcosθ+Omg−QsinθCP+Qcosθmg+QsinθDΨnθ−Qmg−Qcosθ - Question 2 - Select One
A block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
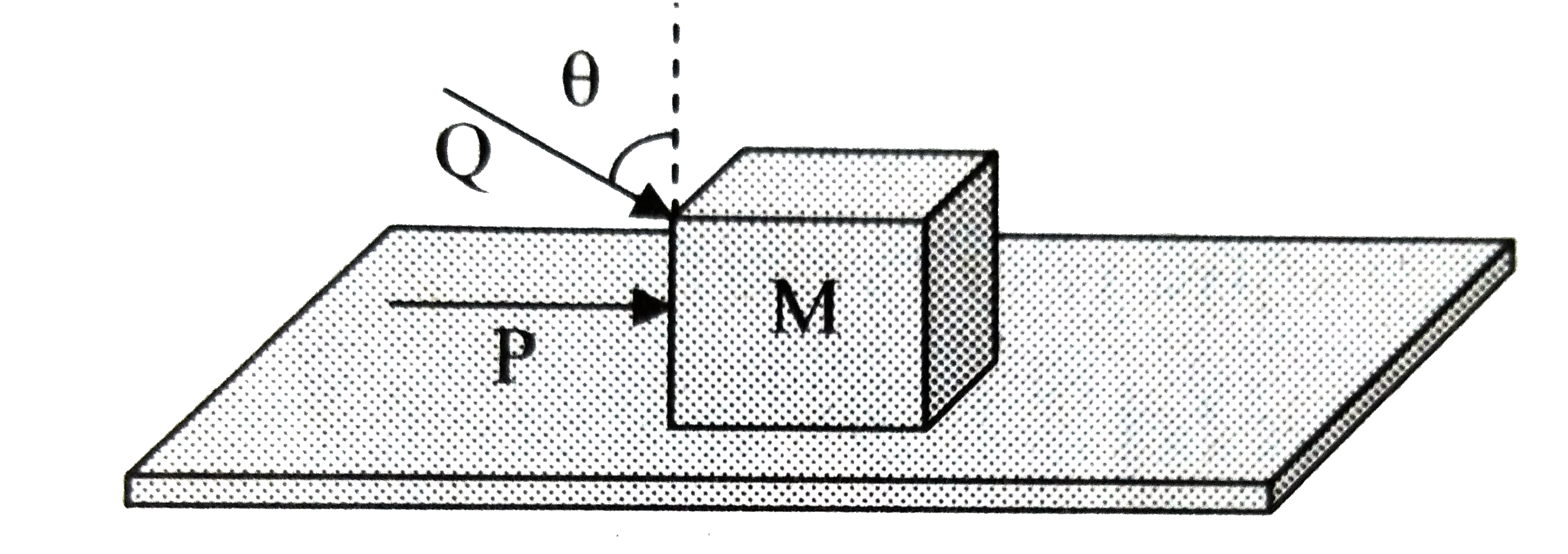 AP+Qsinθmg+QcosθBPcosθ+Qmg−QsinθCP+Qcosθmg+QsinθDPsinθ+Qmg−Qcosθ
AP+Qsinθmg+QcosθBPcosθ+Qmg−QsinθCP+Qcosθmg+QsinθDPsinθ+Qmg−Qcosθ - Question 3 - Select One
A block of mass m lying on a horizontal plane , is acted upon by a horizontal force p and another force Q inclined at an angle θ to the vertical .The block will remain in equilibrium if the coefficient of friction between it and the surface is (assume p>Q)
 A(Psinθ−Q)/(mg−cosθ)B(P−Qsinθ)/(mg+cosθ)C(Pcosθ+Q)/(mg−cosθ)D(P+Qsinθ)/(mg+Qcosθ)
A(Psinθ−Q)/(mg−cosθ)B(P−Qsinθ)/(mg+cosθ)C(Pcosθ+Q)/(mg−cosθ)D(P+Qsinθ)/(mg+Qcosθ)
A block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
 View Solution
View SolutionTwo forces of 5N and 7N act on a aprticle with an angle of 60∘ between them. Find the resultant force.
View SolutionResolve horizontally and vertically a force f =8 N which makes an angle of 45∘ with the horizontal.
View SolutionTwo forces of 12 N and 5 N are acting on a particle , with an angle of 60∘ between them , Calculate the resultant force .
View SolutionTwo forces each of magnitude 2N, act at an angle of 60∘. What is the magnitude of the resultant force ?
View Solution


