If a and b are not perpendicular to each other and , then r is equal to
for all scalars x
none of these
The correct Answer is:C
To solve the problem, we need to analyze the given conditions and derive the value of vector r.
1. Given Conditions:
- We have two vectors a and b that are not perpendicular to each other.
- The equations provided are:
r×a=b×a
r⋅c=0
2. Understanding the Cross Product:
- The equation r×a=b×a implies that the vector r can be expressed in terms of b and some scalar multiple of a.
- Rearranging gives:
r×a−b×a=0
- This indicates that r−b is parallel to a. Therefore, we can write:
r=b+λa
where λ is some scalar.
3. Using the Dot Product Condition:
- The second condition states r⋅c=0. Substituting r from the previous step gives:
(b+λa)⋅c=0
- Expanding this, we have:
b⋅c+λ(a⋅c)=0
4. Solving for λ:
- Rearranging the equation gives:
λ(a⋅c)=−b⋅c
- Thus, we can express λ as:
λ=−b⋅ca⋅c
- This is valid as long as a⋅c≠0.
5. Final Expression for r:
- Substituting λ back into the expression for r:
r=b−b⋅ca⋅ca
Conclusion:
Thus, the vector r can be expressed as:
r=b−b⋅ca⋅ca
- We have two vectors a and b that are not perpendicular to each other.
- The equations provided are:
r×a=b×a
r⋅c=0
- The equation r×a=b×a implies that the vector r can be expressed in terms of b and some scalar multiple of a.
- Rearranging gives:
r×a−b×a=0
- This indicates that r−b is parallel to a. Therefore, we can write:
r=b+λa
where λ is some scalar.
- The second condition states r⋅c=0. Substituting r from the previous step gives:
(b+λa)⋅c=0
- Expanding this, we have:
b⋅c+λ(a⋅c)=0
- Rearranging the equation gives:
λ(a⋅c)=−b⋅c
- Thus, we can express λ as:
λ=−b⋅ca⋅c
- This is valid as long as a⋅c≠0.
- Substituting λ back into the expression for r:
r=b−b⋅ca⋅ca
Thus, the vector r can be expressed as:
r=b−b⋅ca⋅ca
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - ADDITION AND MULTIPLICATION OF VECTORS EXERCISE - Problem Set (2) (TRUE AND FALSE)20videos
ADDITION AND MULTIPLICATION OF VECTORS
- BOOK - ML KHANNACHAPTER - ADDITION AND MULTIPLICATION OF VECTORS EXERCISE - Problem Set (2) (FILL IN THE BLANKS)23videos
ADDITION AND MULTIPLICATION OF VECTORS
- BOOK - ML KHANNACHAPTER - ADDITION AND MULTIPLICATION OF VECTORS EXERCISE - Problem Set (1) (FILL IN THE BLANKS )3videos
ADDITION AND MULTIPLICATION OF VECTORS
- BOOK - ML KHANNACHAPTER - AREA OF CURVESEXERCISE - SELF ASSESSEMENT TEST16videos
AREA OF CURVES
Similar Questions
Knowledge Check
- Question 1 - Select One
If a is perpendicular to b , then the vector a xx { a xx (a xx b) } is equal to
A∣∣a2∣∣bB|a|bC∣∣a3∣∣bD∣∣a4∣∣b - Question 2 - Select One
If a makes an acute angle with b and r×b=c×b, then r is equal to
Aa׈i−bBc×aCc−c.ab.a.bDc+c.ab.ab - Question 3 - Select One
The vectors a and b are not perpendicular and c and d are two vectors satisfying b×c−b×d and a⋅d=0 Then the vector d is equal to
Ac+(a⋅ca⋅b)bBb+(b⋅ca⋅b)cCc−(a⋅ca⋅b)bDb−(b⋅ca⋅b)c
If the non-zero vectors a and b are perpendicular to each other, then the solution of the equation, r×a=b is given by
View SolutionTwo vectors a and b are not perpendicular and c and d are two vectors satifying b×c=b×danda.d=0 Then vector d is equal to
View SolutionIf a=2i+j+k,b=i+2j+k,c=2i−3j+4k and r is a vector such that r×b=c×b and r.a = 0 then r is equal to
View SolutionThe regression lines will be perpendicular to each other if the coefficient of correlation r is equal to
View SolutionCalculate the coefficient of rank correlation.
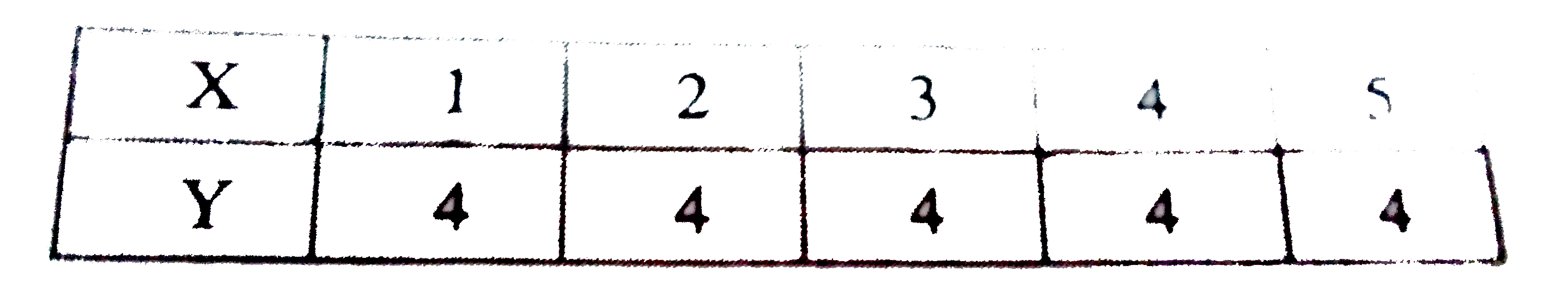 View Solution
View Solution

