The value of θ lying between 0 and π2 and satisfying the equation
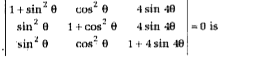
7π24or11π24
5π24
3π24
none of these
The correct Answer is:A
Step by step video, text & image solution for The value of theta lying between 0 and pi/2 and satisfying the equation by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGONOMETRICAL EQUATIONS BOOK - ML KHANNACHAPTER - TRIGONOMETRICAL EQUATIONS EXERCISE - MISCELLANEOUS EXERCISE (MATCHING ENTRIES)
2 Videos
- THEORY OF QUADRATIC EQUATIONS BOOK - ML KHANNACHAPTER - THEORY OF QUADRATIC EQUATIONS EXERCISE - Self Assessment Test
27 Videos
- TRIGONOMETRY RATIOS AND IDENTITIESBOOK - ML KHANNACHAPTER - TRIGONOMETRY RATIOS AND IDENTITIESEXERCISE - MISCELLANEOUS EXERCISE (FILL IN THE BLANKS)
6 Videos
Similar Questions
The value of θ lying between θ=0andπ/2 and satisfying the equation ∣∣ ∣ ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣ ∣ ∣∣=0 are
View SolutionThe value of θ lying between θ=0 and π2 and satisfying the equation.
∣∣ ∣ ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣ ∣ ∣∣
View Solution
Knowledge Check
A value of θ lying between θ=0 and θ=π/2 satisfying the equation
∣∣ ∣ ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣ ∣ ∣∣=0 isA3π/24B5π/24C11π/24Dπ/24The values of θ in between 0∘ and 360∘ and satisfying the equation tanθ+1√3=0 is equal to
Aθ=150∘and300∘Bθ=120∘and300∘Cθ=60∘and240∘Dθ=150∘and330∘The value of θ lying between θ=0andθ=π2 and satisfying the equation
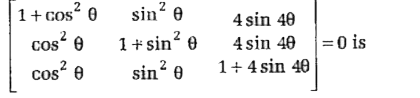 A11π24B7π24C5π24Dπ24
A11π24B7π24C5π24Dπ24
The value of θ lying between θ=0andthη=π2 and satisfying the equation ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣=0are 7π24 (b) 5π24 (c) 11π24 (d) π24
View SolutionFind all values of θ lying between 0 and 2π satisfying the equation rsinθ=√3 and r+4sinθ=2(√3+1)
View SolutionThe value of θ lying between θ=0 and θ=π2 and satisfying the equation ∣∣ ∣ ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣ ∣ ∣∣=0 are
View SolutionThe value of θ lying between 0 and π2 and satisfying ∣∣ ∣ ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣ ∣ ∣∣=0
View SolutionNumber of values of θ lying between θ=0andθ=π satisfying the equation ∣∣ ∣ ∣∣1+sin2θcos2θ4sin6θsin2θ1+cos2θ4sin6θsin2θcos2θ1+4sin6θ∣∣ ∣ ∣∣=0 is
View Solution
