Are the following sets of ordered pairs functions? If so, examine whether the mapping is surjective or injective:
{(a,b): a is a person, b is an ancestor of a}
To determine whether the set of ordered pairs {(a,b): a is a person, b is an ancestor of a} represents a function, we need to analyze the relationship between the elements of the two sets involved: the set of persons (A) and the set of ancestors (B).
1. Definition of a Function:
A relation is a function if every element in the domain (set A) is associated with exactly one element in the codomain (set B). In other words, for every person (a), there should be one and only one ancestor (b).
2. Understanding the Ordered Pairs:
In our case, the ordered pairs consist of a person (a) and their ancestor (b). An ancestor can be defined as a parent, grandparent, great-grandparent, etc.
3. Analyzing the Ancestor Relationship:
For any given person (a), there can be multiple ancestors (b). For example:
- If a is a child, b could be the mother, father, grandfather, grandmother, etc.
- If we consider a grandchild, there could be multiple grandparents.
4. Conclusion on Functionality:
Since a single person (a) can have multiple ancestors (b), this means that there is not a unique mapping from each element of set A (persons) to set B (ancestors). Therefore, the relation does not satisfy the definition of a function.
5. Final Determination:
Since the set of ordered pairs does not meet the criteria for being a function, we conclude that the set is not a function.
A relation is a function if every element in the domain (set A) is associated with exactly one element in the codomain (set B). In other words, for every person (a), there should be one and only one ancestor (b).
In our case, the ordered pairs consist of a person (a) and their ancestor (b). An ancestor can be defined as a parent, grandparent, great-grandparent, etc.
For any given person (a), there can be multiple ancestors (b). For example:
- If a is a child, b could be the mother, father, grandfather, grandmother, etc.
- If we consider a grandchild, there could be multiple grandparents.
Since a single person (a) can have multiple ancestors (b), this means that there is not a unique mapping from each element of set A (persons) to set B (ancestors). Therefore, the relation does not satisfy the definition of a function.
Since the set of ordered pairs does not meet the criteria for being a function, we conclude that the set is not a function.
Topper's Solved these Questions
- FUNCTIONSBook:ML KHANNAChapter:FUNCTIONSExercise:PROBLEM SET (3)
Explore 71 Videos
- FUNCTIONSBook:ML KHANNAChapter:FUNCTIONSExercise:PROBLEM SET (4)
Explore 43 Videos
- FUNCTIONSBook:ML KHANNAChapter:FUNCTIONSExercise:SELF ASSESSMENT TEST
Explore 10 Videos
- EXPONENTIAL AND LOGARITHMIC SERIES Book:ML KHANNAChapter:EXPONENTIAL AND LOGARITHMIC SERIES Exercise:Problem Set (2) (Self Assessment Test)
Explore 8 Videos
- HEIGHTS AND DISTANCESBook:ML KHANNAChapter:HEIGHTS AND DISTANCESExercise:Problem Set (3) FILL IN THE BLANKS
Explore 9 Videos
Similar Questions
Are the following sets of ordered pairs functions? If so, examine whether the mapping is surjective or injective:
{(x, y):x is a person, y is the mother of x}
View SolutionAre the following sets of ordered pairs functions? If so, examine whether the mapping is surjective or injective:
{(x, y):x is a person, y is the mother of x}
View Solution
Knowledge Check
Which of the following function is surjective but not injective?
Af:R→R,f(x)=x4+2x3−x2+1Bf:R→R,f(x)=x3+x+1Cf:R→R+,f(x)=√1+x2Df:R→R,f(x)=x3+2x2−x+1Which of the following function is surjective but not injective?
Af:R→R,f(x)=x4+2x3−x2+1Bf:R→R,f(x)=x3+x+1Cf:R→R,f(x)=√1+x2Df:R→R,f(x)=x3+2x2−x+1Which of the following pairs of months is used in Isothermal maps to examine extremes of temperature.
ADecember and JuneBNovember and JulyCNovember and JuneDJanuary and July
Are the following set of ordered pairs functions? If so, examine whether the mapping is injective or surjective: {(x, y):x is a person, y is the mother of x} (ii) {(a, b):a is a person, b is an ancestor of a}
View SolutionExamine whether the following statements are true or false :
{a,b}⊂{b,c,a}
View SolutionExamine whether the binary operation ∗ defined on R by a∗b=ab+1 is associative or not.
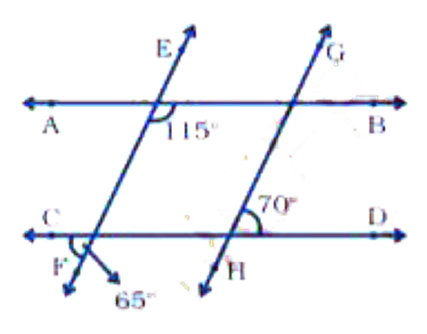
View SolutionIn Fig. 5.63, examine whether the following pairs of lines are parallel or not:
(i) EF and GH (ii) AB and CD
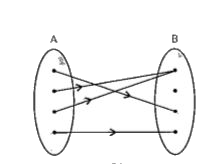
View SolutionThe function f:A→B, defined by a mapping below, is:
View Solution
