A force √5 units acts along the line x−32=y−4−1 , the moment of the force about the point (4,1) along z-axis is
zero
5√5
−√5
5
The correct Answer is:D
Similar Questions
A force of magnitude 6 acts along the vector (9,6,−2) and passes through a point A(4,−1,−7). Then moment of force about the point O(1,−3,2) is
View SolutionFind the moment about the point (3, 4, 5) of the force through the point (1,2,−3) having components equal to −2,3,−4. What is the moment of the same force about the line through the origin having direction - ratios <4,−2,5> ?
View Solution
Knowledge Check
Force of 1, 2 units act along the lines x=0 and y= 0, the equation of the line of acting of the resultants is
Ay−2x=0B2y−x=0Cy+x=0Dy−x=0Force ˆi+2ˆj−3ˆk,2ˆi+3ˆj+4ˆk and −ˆi−ˆj+ˆk are acting at the point P(0,1,2) . The moment of these forces about the point A(1,-2,0) is
A2ˆi−6ˆj+10ˆkB−2ˆi+6ˆj−10ˆkC2ˆi+6ˆj−10ˆkDnone of theseA force of magnitude 6 acts along the vector (9,6,−2) and passes through a point A(4,−1,−7). Then moment of force about the point O(1,−3,2) is
A15011(2ˆi−3ˆj)B611(50ˆi−75ˆj+36ˆk)C150(2ˆi−3ˆk)D6(50ˆi−75ˆj+36ˆk)
IF the force represented by 3ˆj+2ˆk is acting through the point 5ˆi+4ˆj−3ˆk , then its moment about th point (1,3,1) is
View SolutionFind the moment about the point (1,-1,-1) of the force 3ˆi+4ˆj−5ˆk acting at the point (1,0,-1)
View SolutionForces of 1 and 2units act along the lines x=0 and y=0. The equation of the line of action of the resultant is
View SolutionThree particles, each of mass m are placed an the points (x1,y1,z1),(x2,y2,z2) and (x3,y3,z3) on the inner surface of a paraboloid of revolution obtained by rotating the parabola x2=4ay about the y-axis. Neglected the mass of the paraboloid. (y-axis. is along the vertical (a) the moment of inertia of the system about the axis of the paraboloid is I=4ma(y1+y2+y3)
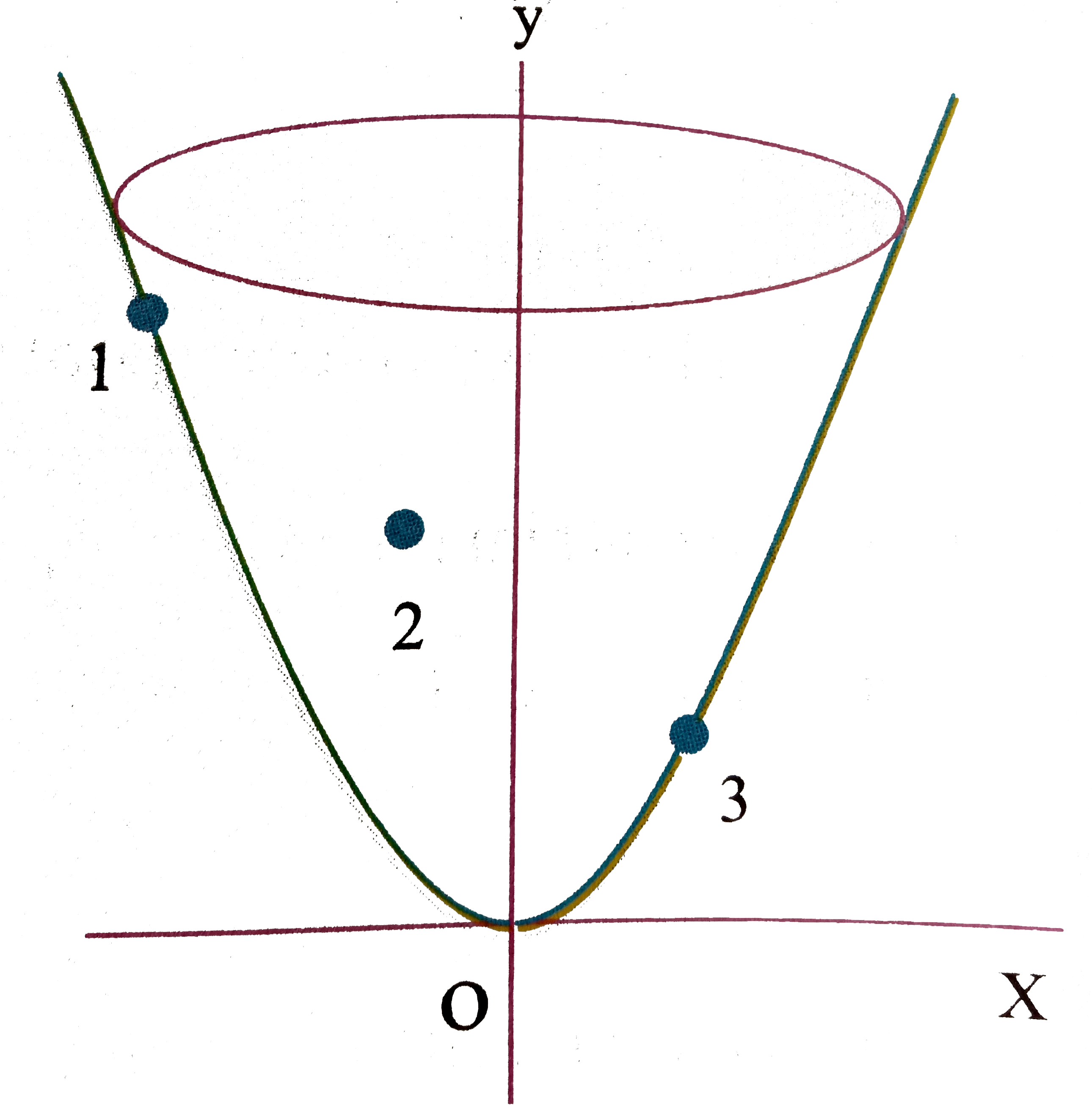
View SolutionIF the force represented by 3ˆi+2ˆk is acting through the point 5ˆi+4ˆj−3ˆk , then its moment about th point (1,3,1) is
View Solution
