Determine the value of (1r+1s) when r3+s3=0 and r + s = 6
0
0.5
1
6
The correct Answer is:B
To solve the problem of determining the value of 1r+1s given that r3+s3=0 and r+s=6, we can follow these steps:
Step 1: Use the identity for the sum of cubes
We know that:
r3+s3=(r+s)(r2−rs+s2)
Given that r3+s3=0, we can set up the equation:
0=(r+s)(r2−rs+s2)
Step 2: Substitute the known value of r+s
Since we know r+s=6, we can substitute this into the equation:
0=6(r2−rs+s2)
This implies:
r2−rs+s2=0
Step 3: Use the identity for r2+s2
We can express r2+s2 in terms of r+s and rs:
r2+s2=(r+s)2−2rs
Substituting r+s=6:
r2+s2=62−2rs=36−2rs
Now, substituting this into the equation from Step 2:
36−2rs−rs=0
This simplifies to:
36−3rs=0
Step 4: Solve for rs
Rearranging gives:
3rs=36⟹rs=363=12
Step 5: Find 1r+1s
We can express 1r+1s as:
1r+1s=s+rrs
Substituting the known values r+s=6 and rs=12:
1r+1s=612=12
Final Answer
Thus, the value of 1r+1s is 12.
---
We know that:
r3+s3=(r+s)(r2−rs+s2)
Given that r3+s3=0, we can set up the equation:
0=(r+s)(r2−rs+s2)
Since we know r+s=6, we can substitute this into the equation:
0=6(r2−rs+s2)
This implies:
r2−rs+s2=0
We can express r2+s2 in terms of r+s and rs:
r2+s2=(r+s)2−2rs
Substituting r+s=6:
r2+s2=62−2rs=36−2rs
Now, substituting this into the equation from Step 2:
36−2rs−rs=0
This simplifies to:
36−3rs=0
Rearranging gives:
3rs=36⟹rs=363=12
We can express 1r+1s as:
1r+1s=s+rrs
Substituting the known values r+s=6 and rs=12:
1r+1s=612=12
Thus, the value of 1r+1s is 12.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - ALGEBRAEXERCISE - Questions Asked In Previous SSC Exams (Type - III)17videos
ALGEBRA
- BOOK - KIRAN PUBLICATIONCHAPTER - ALGEBRAEXERCISE - Questions Asked In Previous SSC Exams (Type - IV)59videos
ALGEBRA
- BOOK - KIRAN PUBLICATIONCHAPTER - ALGEBRAEXERCISE - Test Yourself25videos
ALGEBRA
- BOOK - KIRAN PUBLICATIONCHAPTER - ALLIGATION OR MIXTURESEXERCISE - TEST YOURSELF27videos
ALLIGATION OR MIXTURES
Similar Questions
Knowledge Check
- Question 1 - Select One
In a triangle ABC, if a−bb−c=s−as−c, then r1,r2,r3 are in
AH.P.BG.P.CA.P.Dnone - Question 2 - Select One
If S=a1−r3, then expres r in terms of S and a.
Ar=3√1+a2Br=3√1+SaCr=3√1−SaDr=3√1−aS - Question 3 - Select One
If r and s are variables satisfying the equation 1r+s=1r+1s. The value of (rs)3 is equal to :
A1B−1C3Dnot possible to determine
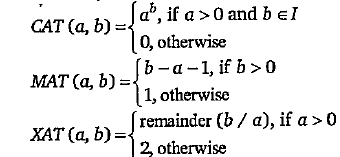
XAT(r,s)MAT(r,s)=2
(i) r = 3, s = 5
(ii) r = -3, s = -5View SolutionIf Sn=n⋅(2n2+9n+13)6 ( Sn = sum of first n terms of the sequence) then the value of ∑∞i=11r√(Sr−Sr−1)
View SolutionDetermine whether the points are collinear
R(0,3),D(2,1),S(3,−1)View SolutionIf R=a3+1a−1 and S=a2−a+1a+1, then R + S is:
View SolutionIf S=a1−r3, then expres r in terms of S and a.
View Solution

