Let f:N→N be a function deifned by f(x)=9x2+6x−5. Show that f:N→S, where S is the range of 'f', is invertible. Find the inverse of 'f' and hence, find f−1(43)andf−1(163)Solution in Punjabi
Step by step video & image solution for Let f : N rarr N be a function deifned by f(x) = 9x^2 + 6x - 5. Show that f : N rarr S, where S is the range of 'f', is invertible. Find the inverse of 'f' and hence, find f^-1(43) and f^-1(163) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RELATIONS AND FUNCTIONBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONEXERCISE - EXAMPLE
212 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EXERCISE
543 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXAMPLE
13 Videos
Similar Questions
Which one of the following graph represents the function of x? Why?
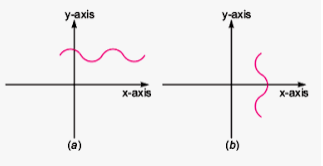
View SolutionCompute P(A∣B),if P(B)=0.5 and P(A∩B)=0.32
View SolutionState the reason for the relation R, in the set {1,2,3} given by R= {(1,2), (2, 1), not to be transitive.
View SolutionLet f:N→R be a function defined as f(x)=4x2+12x+15. Show that f:N→S, where, S is the range of f, is invertible. Find the inverse of f.
View SolutionLet f:N→S be a function defined as f(x)=9x2+6x−5. Show that f:N→S, where S is the range of f is invertible. Find the inverse of f and hence f−1(43)andf−1(163)
View SolutionLet f:N→Y:f(x)=x2 where Y= range (f). Show that f is invertible and find f−1
View SolutionLet f:N→R be a function defined as f(x)=4x2+12x+15. Show that f:N→S. where, S is the range of f, is invertible. Find the inverse of f.
View SolutionLet f:N→R be a function defined as f'(x)=4x2+12x+15. Show that f:N→S. where, S is the range of f, is invertible. Find the inverse of f.
View SolutionLet f:N→R be a function defined as f'(x)=4x2+12x+15. Show that f:N→S. where, S is the range of f, is invertible. Find the inverse of f.
View SolutionLet f:N→Rbe a function defined as f(x)=4x2+12x+15. Show that f:N→S, where, S is the range of f, is invertible. Find the inverse of f.
View SolutionLet f:N→R be a function defined as f(x)=4x2+12x+15. Show that f:N→S, where S is the range of f is invertible. Also find the inverse of f
View SolutionLet f:N→S be a function defined as f(x)=9x2+6x−5. Show that f:N→S, where S is the range of f , is invertible. Find the inverse of f and hence f−1(43)andf−1(163)
View SolutionLet f:N→Rbe a function defined as f(x)=4x2+12x+15. Show that f:N→S, where, S is the range of f, is invertible. Find the inverse of f.
View SolutionLet f:N→ be a function defined as f(x)=9x2+6x−5. Show that f:N→S, where S is the range of f, is invertible. Find the inverse of f and hence f−1(43) and f−1(163).
View Solutionf:N→R,f(x)=4x2+12x+5. Show that f:N→R is invertible function . Find the inverse of f.
View SolutionLet f':N→R be a function defined as f'(x)=4x2+12x+15 . Show that f:N→S , where, S is the range of f, is invertible. Find the inverse of f.
View Solution
