Show that each of the relation R in the set A ={x∈z:0≤x≤12}, given by
R = {(a,b) : |a-b| is a multiple of 4} is an equivalec relation. Find the set of all elements related to 1 in each case.Solution in Punjabi
Step by step video & image solution for Show that each of the relation R in the set A ={x in z : 0 le x le 12}, given by R = {(a,b) : |a-b| is a multiple of 4} is an equivalec relation. Find the set of all elements related to 1 in each case. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RELATIONS AND FUNCTIONBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONEXERCISE - EXAMPLE
212 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EXERCISE
543 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXAMPLE
13 Videos
Similar Questions
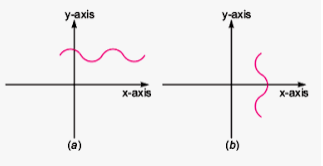
Which one of the following graph represents the function of x? Why?
View SolutionCompute P(A∣B),if P(B)=0.5 and P(A∩B)=0.32
View SolutionState the reason for the relation R, in the set {1,2,3} given by R= {(1,2), (2, 1), not to be transitive.
View Solutionसिद्ध किजिए कि समुच्चय A={x∈Z:0≤x≤12} में दिए गए निम्नलिखित संबंधों R में से प्रत्येक एक तुल्यता संबंध हैं:
(i) R = {(a, b) : la-bl, 4 का एक गुणज है
(ii) R = { (a, b) a = b},
प्रत्येक दशा में । से संबंधित अवयवों को ज्ञात कीजिए।
View Solutionसिद्ध कीजिये कि समुच्चय A={x∈Z,0≤x≤12} में प्रदत्त संबंध R={(a,b):a=b} एक तुल्यता संबंध है। 1 से संबंधित अवयवों को ज्ञात कीजिये।
View SolutionShow that the relation R, on the set
A={x∈Z:0≤x≤12} given by R = {(a,b) : |a-b| is a multiple of 4 and a,b ∈ A } is an equivalance relation on A.
View SolutionShow that the relation R in the set A={x∈Z:0≤x≤12} given by R={a,b):|a−b| is a multiple of 4} is an equivalence relation.
View SolutionShow that the relation R in the set A={x∈z,0≤x≤12} given by R={ab|a−b∣ is a multiple of 4} is an equivalence relation.
View SolutionLet R be the relation on set A={x:x∈Z,0≤x≤10} given by R={(a,b):(a−b)is divisible by 4}. Show that R is an equivalence relation.
Also, write all elements related to 4.
View SolutionShow that each of the relation R in set A={x∈Z:0≤x≤12}, given by
(i) R={(a,b):|a−b| is a multiple of 4}
(ii) R={(a,b):a=b}
is an equivalence relation. Find the set of all elements related to 1 in each case.
View SolutionShow that the relation R in the set A={1,2,3,4,5} given by
R={(a,b):|a−b| is even}, is an equivalence relation. Show that all the elements of {1,3,5} are related to each other and all the elements of {2,4} are related to each other. But no element of {1,3,5} is related to any element of {2,4}.
View SolutionShow that each of the relation R in set A={x∈Z:0≤x≤12}, given by
(i) R={(a,b):|a−b| is a multiple of 4}
(ii) R={(a,b):a=b}
is an equivalence relation. Find the set of all elements related to 1 in each case.
View SolutionShow that each of the relation R in set A={x∈Z:0≤x≤12}, given by
(i) R={(a,b):|a−b| is a multiple of 4}
(ii) R={(a,b):a=b}
is an equivalence relation. Find the set of all elements related to 1 in each case.
View SolutionShow that the relation R in the set : R={x:x∈Z,0≤x≤12}, given by : R={(a,b):a=b} are equivalence relations.
View SolutionShow that each of the relation R in the set A={x∈Z:0≤x≤12} given by
R={ab|a−b∣ is multiple of 4} is in equivelance.
View SolutionShow that each of the relation R in the set A={x∈Z:0≤x≤12} given by
R={(a,b):a=b} is an equivalence relation . Find the set of all elements related to 1 each case.
View Solution
