State whether the following statements are true or false. Justify. If * is a commutative binary operation on N, then a*(b*c) = (c*b)*aSolution in Punjabi
Step by step video & image solution for State whether the following statements are true or false. Justify. If * is a commutative binary operation on N, then a*(b*c) = (c*b)*a by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RELATIONS AND FUNCTIONBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONEXERCISE - EXAMPLE
212 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EXERCISE
543 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXAMPLE
13 Videos
Similar Questions
Which one of the following graph represents the function of x? Why?
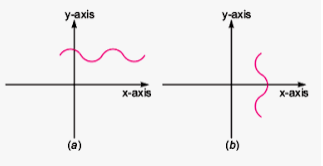
View SolutionCompute P(A∣B),if P(B)=0.5 and P(A∩B)=0.32
View SolutionState the reason for the relation R, in the set {1,2,3} given by R= {(1,2), (2, 1), not to be transitive.
View SolutionState whether the following statements are true or false. Justify.
(i) For an arbitrary binary operation ∗ on a set N, a∗a=a∀a∈N.
(ii) If ∗ is a commutative binary operation on N, then a∗(b∗c)=(c∗b)∗a
View Solutionबतलाइए कि क्या निम्नलिखित कथन सत्य हैं या असत्य है। औचित्य भी बतलाइए।
(i) समुच्चय N में किसी भी स्वेच्छ द्विआधारी संक्रिया * के लिए , a∗a=a,∀a∈N
(ii )यदि N में * एक क्रमविनिमेय द्विआधारी संक्रिया है, तो a∗(b∗c)=(c∗b)∗a
View Solutionबताइए कि क्या कथन सत्य है या असत्य है। औचित्य भी बताइए ।
यदि N में ∗ एक क्रमविनिमेय द्विआधारी संक्रिया है, तो a∗(b∗c)=a∗(c∗b)=(c∗b)∗a
View SolutionState whether the following statements are true or false with reasons.
(i) For any binary operation ∗ on N, a∗a=a∀a∈N.
(ii) If ∗, a binary operation ∗ on N is commutative then, a∗(b∗c)=(c∗b)∗a.
View Solutionयदि N में ∗ एक क्रम - विनिमेय द्वि - आधारी संक्रिया है, तो दर्शाइए
a∗(b∗c)=(c∗b)∗a
View SolutionState whether the following statements are true or false, Justify.
(i) For an arbitraty binary opertion ∗on a set N,a∗a=a∀a∈N.
(ii) If ∗ is a commutative binary opertion on N, then a∗(b∗c)=(c∗b)∗a
View SolutionState whether the following statements are true or false, Justify.
If ∗ is a commutative binary opertion on N, then a∗(b∗c)=(c∗b)∗a
View SolutionState whether the following statements are true or false, Justify.
(i) For an arbitrary binary operation ∗on a set N,a∗a=a∀a∈N.
(ii) If ∗ is a commutative binary opertion on N, then a∗(b∗c)=(c∗b)∗a
View SolutionState whether the following statements are true or false, Justify.
(i) For an arbitraty binary opertion ∗on a set N,a∗a=a∀a∈N.
(ii) If ∗ is a commutative binary opertion on N, then a∗(b∗c)=(c∗b)⋅8a
View SolutionState whether the following statements are true or false. Justify.
(i) For an arbitrary binary operation ∗ on a set N, a∗a=a∀a∈N.
(ii) If ∗ is a commutative binary operation on N, then a∗(b∗c)=(c∗b)∗a
View SolutionState whether the following statements are true or false . Justify .
For an arbitrary binary operation ∗ on a set N, a*a=a∀a∈N.
View SolutionState whether the following statements are true or false . Justify .
If ∗ is commutative binary operation on N, then a*(b*c)=(c*b)*a.
View SolutionState whether the following statements are true or false. Justify
For an arbitary binary operation ∗ on N, a∗a=a∀a∈N
View Solution
