Question

The number of acyclic structural isomers (including geometrical isomers) for pentene are _____

Explanation

To determine the number of acyclic structural isomers (including geometrical isomers) for pentene (C5H10), we will follow these steps:

Step 1: Identify the structure of pentene
Pentene is an alkene with the formula C5H10. It contains one double bond. The general structure of pentene can be represented as follows:

\( \text{C}_n\text{H}_{2n} \)

For pentene (n=5), the formula is C5H10.

Step 2: Determine the position of the double bond
The double bond in pentene can be located at different positions. The possible positions for the double bond in pentene are:

1. 1-pentene: The double bond is between the first and second carbon atoms.
\( \text{CH}_2= \text{CH}-\text{CH}_2-\text{CH}_2-\text{CH}_3 \)

2. 2-pentene: The double bond is between the second and third carbon atoms.
\( \text{CH}_3-\text{CH}=\text{CH}-\text{CH}_2-\text{CH}_3 \)

3. 3-pentene: The double bond is between the third and fourth carbon atoms.
\( \text{CH}_3-\text{CH}_2-\text{CH}=\text{CH}-\text{CH}_3 \)

Step 3: Consider geometrical isomers
For 2-pentene, we can have geometrical isomers due to the presence of the double bond. The two geometrical isomers are:

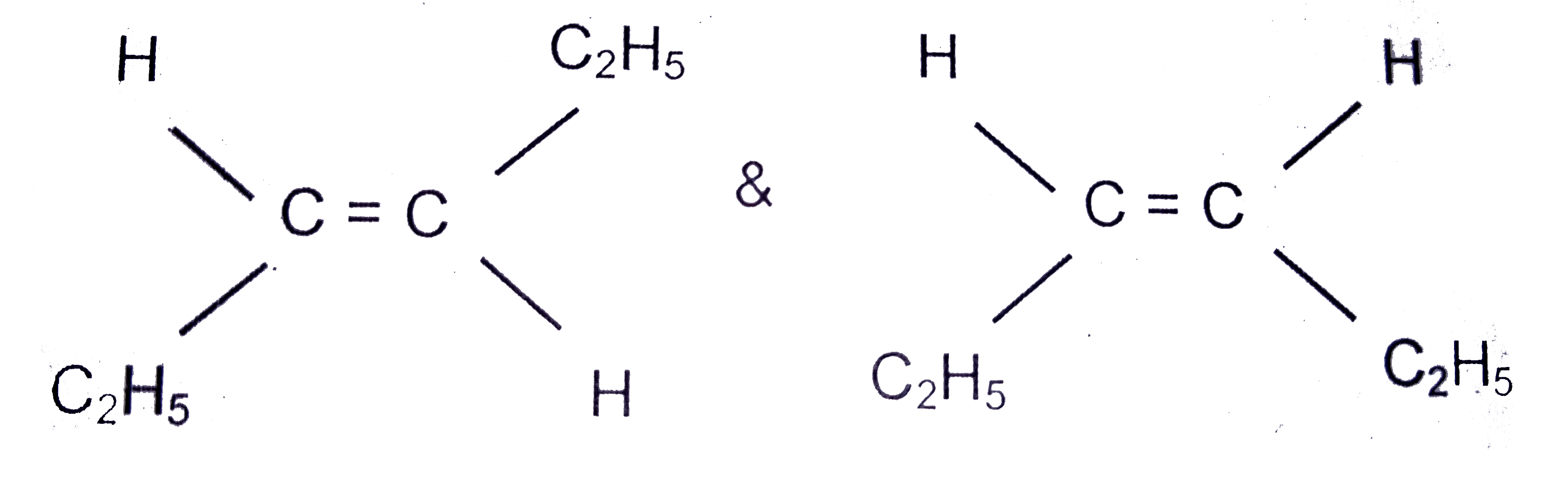
1. Cis-2-pentene: The two methyl groups (CH3) are on the same side of the double bond.
2. Trans-2-pentene: The two methyl groups (CH3) are on opposite sides of the double bond.

Step 4: List all structural isomers
Now we can summarize the structural isomers we have identified:

1. 1-pentene
2. Cis-2-pentene
3. Trans-2-pentene
4. 3-pentene

Step 5: Count the total number of isomers
Now, we can count the total number of acyclic structural isomers, including geometrical isomers:

- 1-pentene: 1 isomer
- Cis-2-pentene: 1 isomer
- Trans-2-pentene: 1 isomer
- 3-pentene: 1 isomer

Thus, the total number of acyclic structural isomers for pentene is 4.

Final Answer
The number of acyclic structural isomers (including geometrical isomers) for pentene is 4.

---