One mole of an ideal gas is taken through an adiabatic process where the temperature rises from 27∘C to 37∘C. If the ideal gas is composed of polyatomic molecule that has 4 vibrational modes, which of the following is true ?
[R=8.314 J mol−1k−1]
work done by the gas is close to 332 J
work done on the gas is close to 582 J
Work done by the gas is close to 582 J
work done on the gas close to 332 J
The correct Answer is:B
To solve the problem, we need to follow these steps:
Step 1: Understand the Given Data
We have 1 mole of an ideal gas undergoing an adiabatic process, with an initial temperature T1=27∘C and a final temperature T2=37∘C. We also know that the gas is polyatomic with 4 vibrational modes.
Step 2: Convert Temperatures to Kelvin
Convert the temperatures from Celsius to Kelvin:
T1=27+273.15=300.15K
T2=37+273.15=310.15K
Step 3: Calculate the Degrees of Freedom (F)
For a polyatomic gas with fv=4 vibrational modes, the total degrees of freedom F can be calculated as:
F=3(translational)+3(rotational)+4×2(vibrational)=3+3+8=14
Step 4: Calculate the Heat Capacity Ratio (γ)
The heat capacity ratio γ is given by:
γ=1+2F
Substituting F=14:
γ=1+214=1+17=87
Step 5: Calculate Work Done in Adiabatic Process
In an adiabatic process, the work done W can be expressed as:
W=nR(T1−T2)γ−1
Substituting the values:
- n=1mol
- R=8.314J/mol⋅K
- T1=300.15K
- T2=310.15K
- γ=87
Calculating W:
W=1×8.314×(300.15−310.15)87−1
=8.314×−1017=8.314×−70=−582.98J
Step 6: Interpret the Result
The negative sign indicates that work is done on the gas. Thus, the magnitude of the work done is approximately 582J.
Conclusion
The work done on the gas is approximately 582J.
---
We have 1 mole of an ideal gas undergoing an adiabatic process, with an initial temperature T1=27∘C and a final temperature T2=37∘C. We also know that the gas is polyatomic with 4 vibrational modes.
Convert the temperatures from Celsius to Kelvin:
T1=27+273.15=300.15K
T2=37+273.15=310.15K
For a polyatomic gas with fv=4 vibrational modes, the total degrees of freedom F can be calculated as:
F=3(translational)+3(rotational)+4×2(vibrational)=3+3+8=14
The heat capacity ratio γ is given by:
γ=1+2F
Substituting F=14:
γ=1+214=1+17=87
In an adiabatic process, the work done W can be expressed as:
W=nR(T1−T2)γ−1
Substituting the values:
- n=1mol
- R=8.314J/mol⋅K
- T1=300.15K
- T2=310.15K
- γ=87
W=1×8.314×(300.15−310.15)87−1
=8.314×−1017=8.314×−70=−582.98J
The negative sign indicates that work is done on the gas. Thus, the magnitude of the work done is approximately 582J.
The work done on the gas is approximately 582J.
Similar Questions
1 mole of an ideal gas undergo adiabatic process which increases temperature from 270C→370C . Gas is polyatomic has 4 vibrational mode of freedom. Find net work
View SolutionHalf mole of an ideal monoatomic gas is heated at constant pressure of 1 atm from 20∘C to 90∘C. Work done by gas is close to: (Gas constant R = 8.31 J/mol-K)
View Solution
Knowledge Check
One mole of an ideal gas (γ=7/5) is adiabatically compressed so that its temperature rises from 27∘C to 35∘C the work done by the gas is (R=8.47J/mol-K)
A−160JB−168JC150JD120JOne mole of an ideal gas is taken through a cyclic process. The minimum temperature during the cycle is 300K. Then, net exchange of heat for complete cycle is
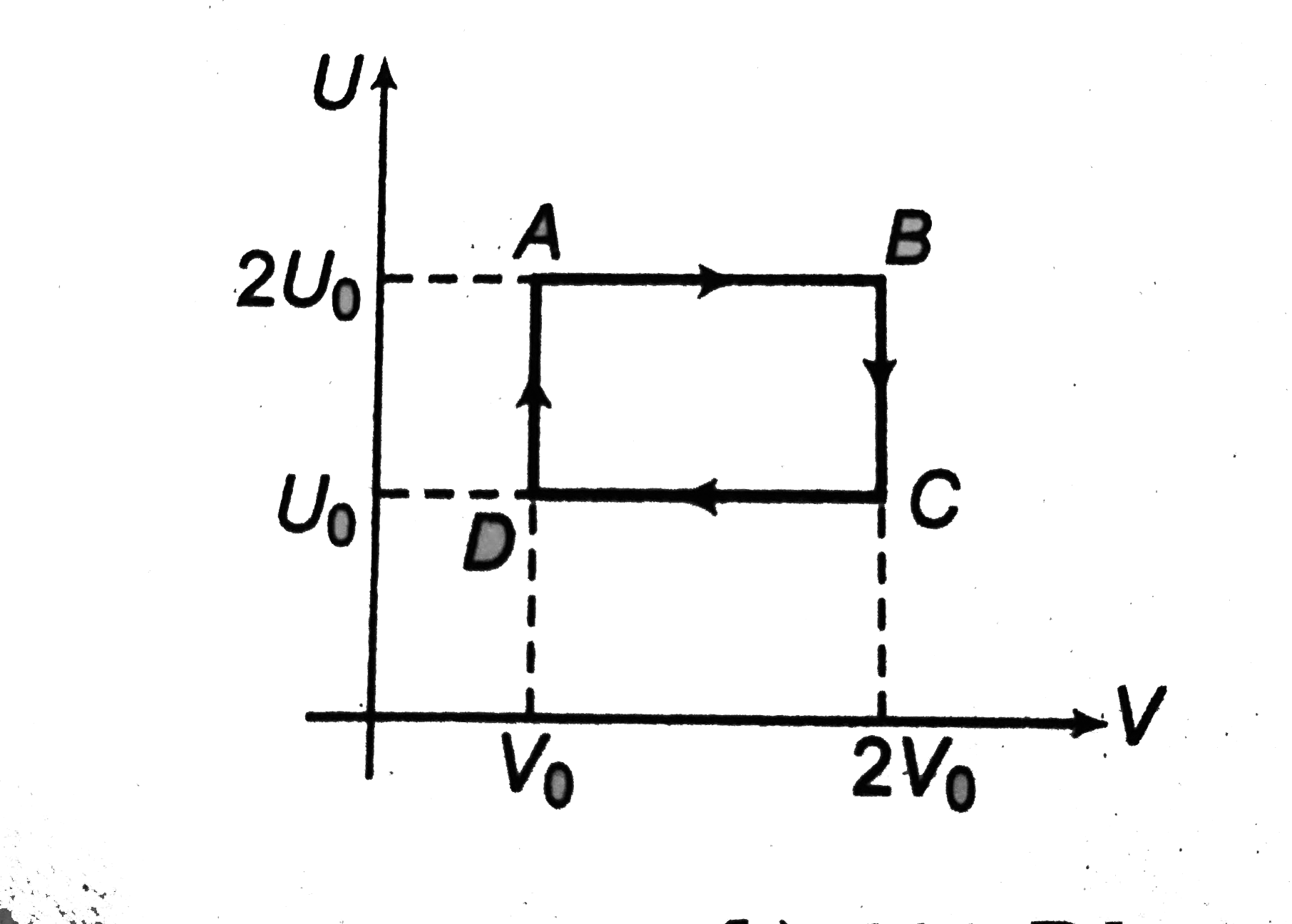 A600Rln2B300Rln2C−300Rln2D900Rln2
A600Rln2B300Rln2C−300Rln2D900Rln2One mole of an ideal gas with γ=1.4 is adiabatically compressed so that its temperature rises from 27∘C to 34∘C . The change in the internal energy of the gas is (R=8.3Jmol−10k−1)
A−166JB166JC168JD−168J
One mole of an ideal gas (γ=1.4) is adiabatically compressed so that its temperature rises from 27∘C to 35∘C. The change in the internal energy of the gas is (given R = 8.3 J/mole K)
View SolutionOne mole of an ideal gas is allowed to expand reversible and adiabatically from a temperatureof27∘C)if the work done during the process is3kJ,the final temperature will be equal to(Cv=20JK−1)
View SolutionOne mole of an ideal gas is taken through a cyclic process as shown in the V-T diagram. Which of the following statements is true ?
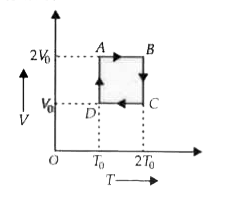
View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
View SolutionOne mole of an ideal monoatomaic gas is taken from A to C along the path ABC . The temperature of the gas at A is T0 . For the process ABC :
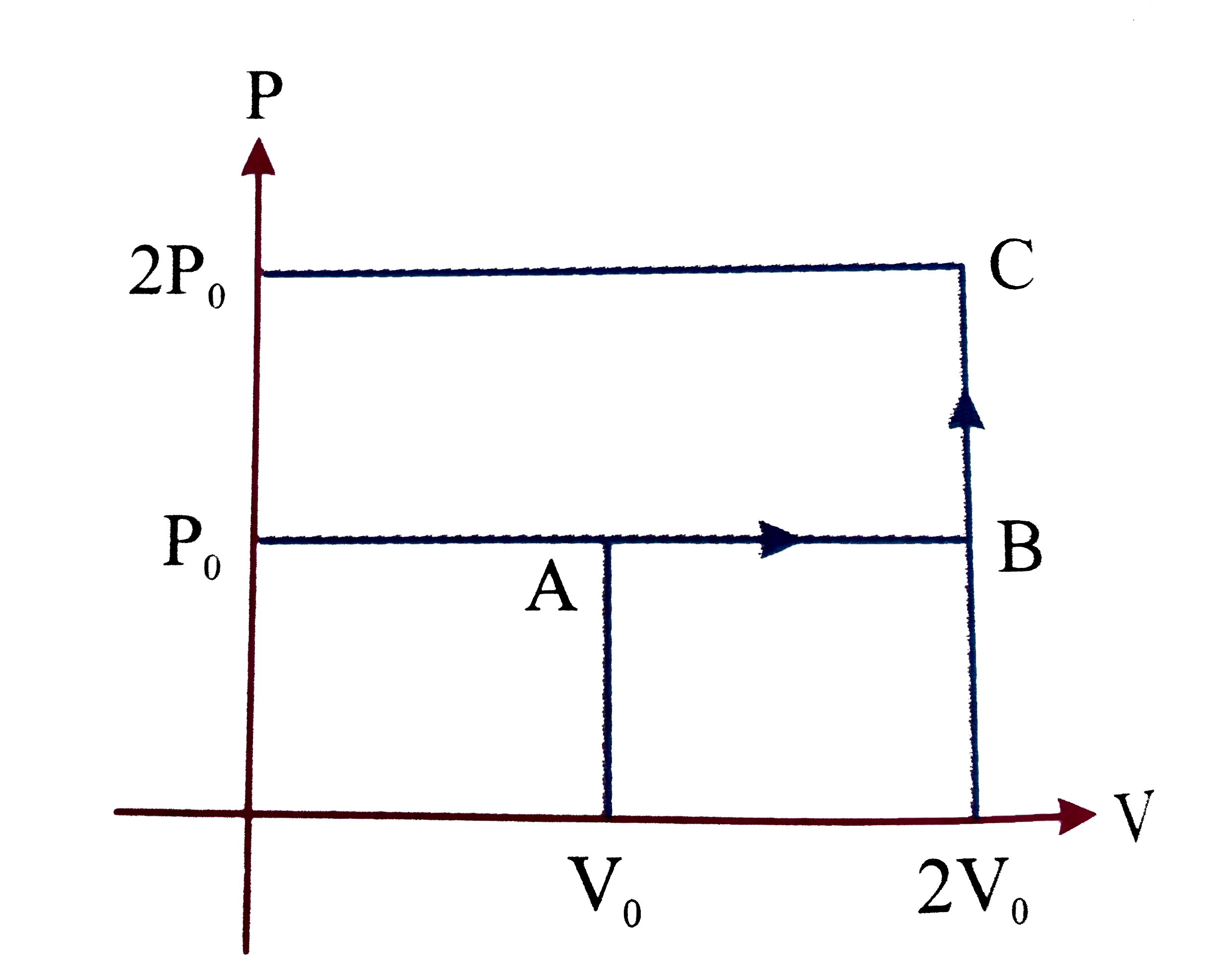
View Solution
