Which of the following is the negation of the statement "for all M>0 , there exists x∈S such that x≥M ?
there exists M>0, such that x< M for all x∈S
there exists M>0, there exists x∈S such that x≥M
there exists M>0, there exists x∈S such that x<M
there exists M>0 , such that x≥M for all x∈S
The correct Answer is:A
To find the negation of the statement "for all M>0, there exists x∈S such that x≥M", we can follow these steps:
Step 1: Understand the Original Statement
The original statement can be broken down as:
- "For all M>0" means that the statement applies to every positive value of M.
- "There exists x∈S" means that for each M, we can find at least one x in the set S.
- "Such that x≥M" means that this x is greater than or equal to M.
Step 2: Identify the Structure of the Statement
The statement has the form:
- Universal quantifier (for all) followed by an existential quantifier (there exists).
Step 3: Apply Negation Rules
The negation of a statement that has the structure "for all M, there exists x" can be transformed using the following rules:
- The negation of "for all" (∀) is "there exists" (∃).
- The negation of "there exists" (∃) is "for all" (∀).
- Additionally, we need to negate the inner condition.
Step 4: Write the Negation
Applying the negation:
1. Start with "for all M>0" and negate it to "there exists M>0".
2. Then negate "there exists x∈S such that x≥M" to "for all x∈S, x<M".
Combining these, we get:
"There exists M>0 such that for all x∈S, x<M".
Step 5: Final Statement
Thus, the negation of the original statement is:
"There exists M>0 such that for all x∈S, x<M".
The original statement can be broken down as:
- "For all M>0" means that the statement applies to every positive value of M.
- "There exists x∈S" means that for each M, we can find at least one x in the set S.
- "Such that x≥M" means that this x is greater than or equal to M.
The statement has the form:
- Universal quantifier (for all) followed by an existential quantifier (there exists).
The negation of a statement that has the structure "for all M, there exists x" can be transformed using the following rules:
- The negation of "for all" (∀) is "there exists" (∃).
- The negation of "there exists" (∃) is "for all" (∀).
- Additionally, we need to negate the inner condition.
Applying the negation:
1. Start with "for all M>0" and negate it to "there exists M>0".
2. Then negate "there exists x∈S such that x≥M" to "for all x∈S, x<M".
"There exists M>0 such that for all x∈S, x<M".
Thus, the negation of the original statement is:
"There exists M>0 such that for all x∈S, x<M".
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - MATHEMATICS (SECTION-B)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Mathematics Section A
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - MATHEMATICS
30 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - MATHEMATICS
250 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - MATHEMATICS (SECTION - B)
10 Videos
Similar Questions
Let S be a non-empty subset of R. Consider the following statement: P: There is a rational number x∈S such that x>0.
Which of the following statements is the negation of the statement P ?
There is no rational number x∈S such that x≤0 (9)
Every rational number x∈S satisfies x≤0 (18)
x∈S and x≤0⇒x (27) is not rational
There is a rational number x∈S such that x≤0 (36)
View SolutionWrite the negation of the following statement: r: There exists a number x such that 0<x<1.
View Solution
Knowledge Check
The negation of the statemen
∀x∈N,x+1>2 isAAA x cancel in N, x + 1 lt 2B∃x∈N, such that x + 1 gt 2C∀x∈N,x+1≤2D∃x∈N, such that x+1≤2The negation of the statement, ∃x∈R such that x2+3>0 , is
A∃x∈R, such that x2+3<0B∀x∈R,x2+3>0C∀x∈R,x2+3<=0D∃x∈R, such that x2+3=0Which of the following to is the common region for x+y≤10,x≥5,y≤10,x≥0andy≥0.
A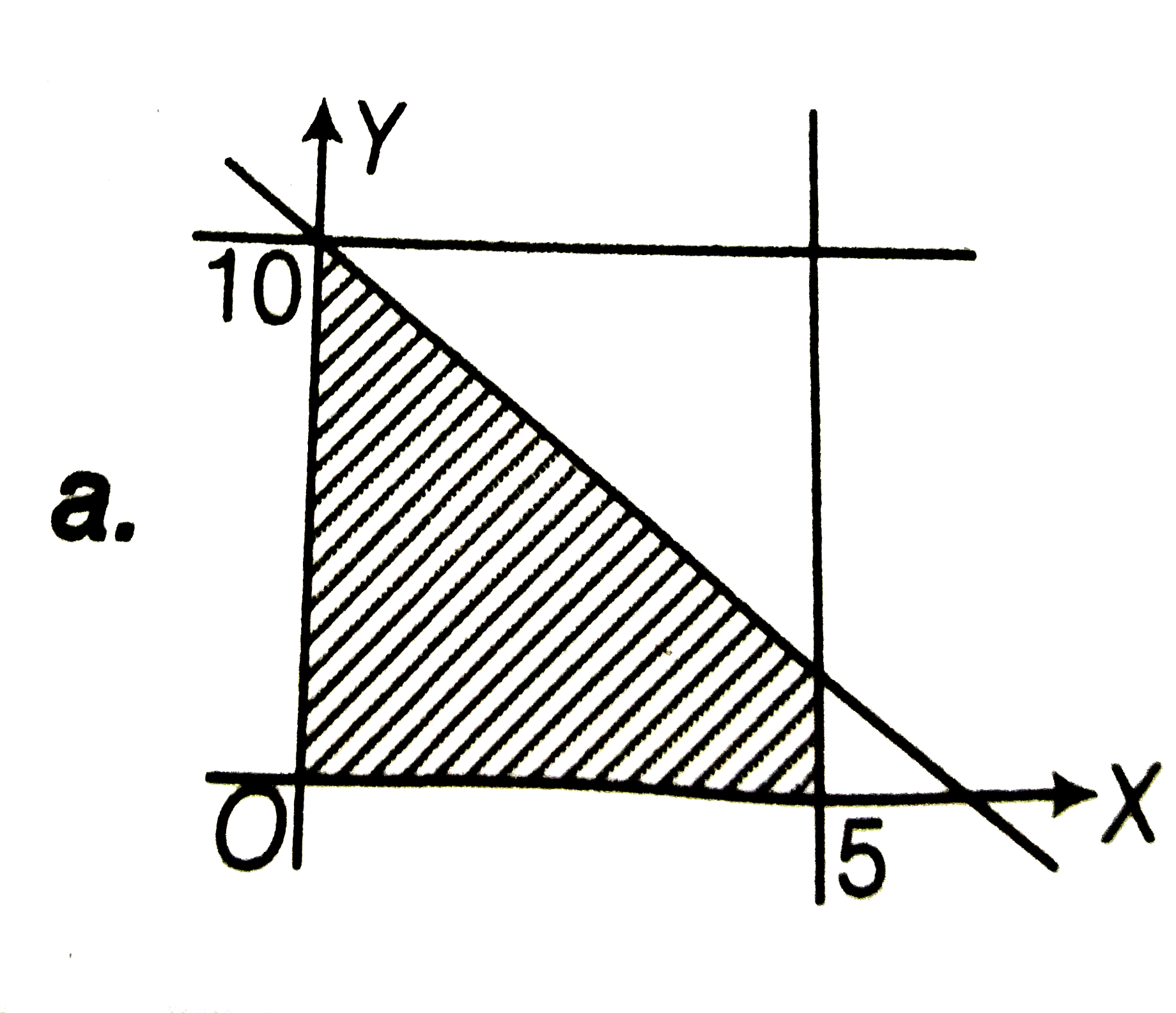 B
B C
C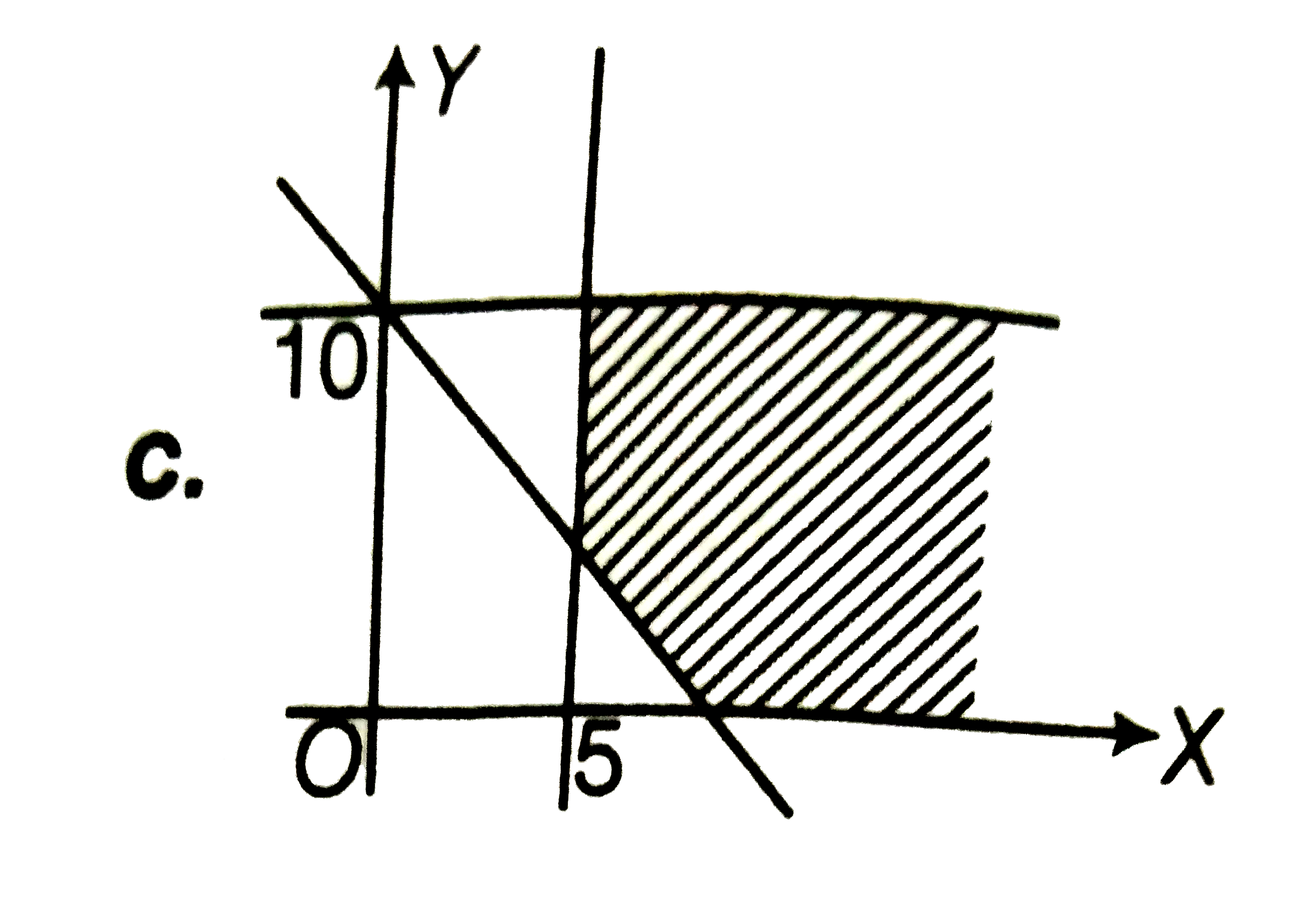 D
D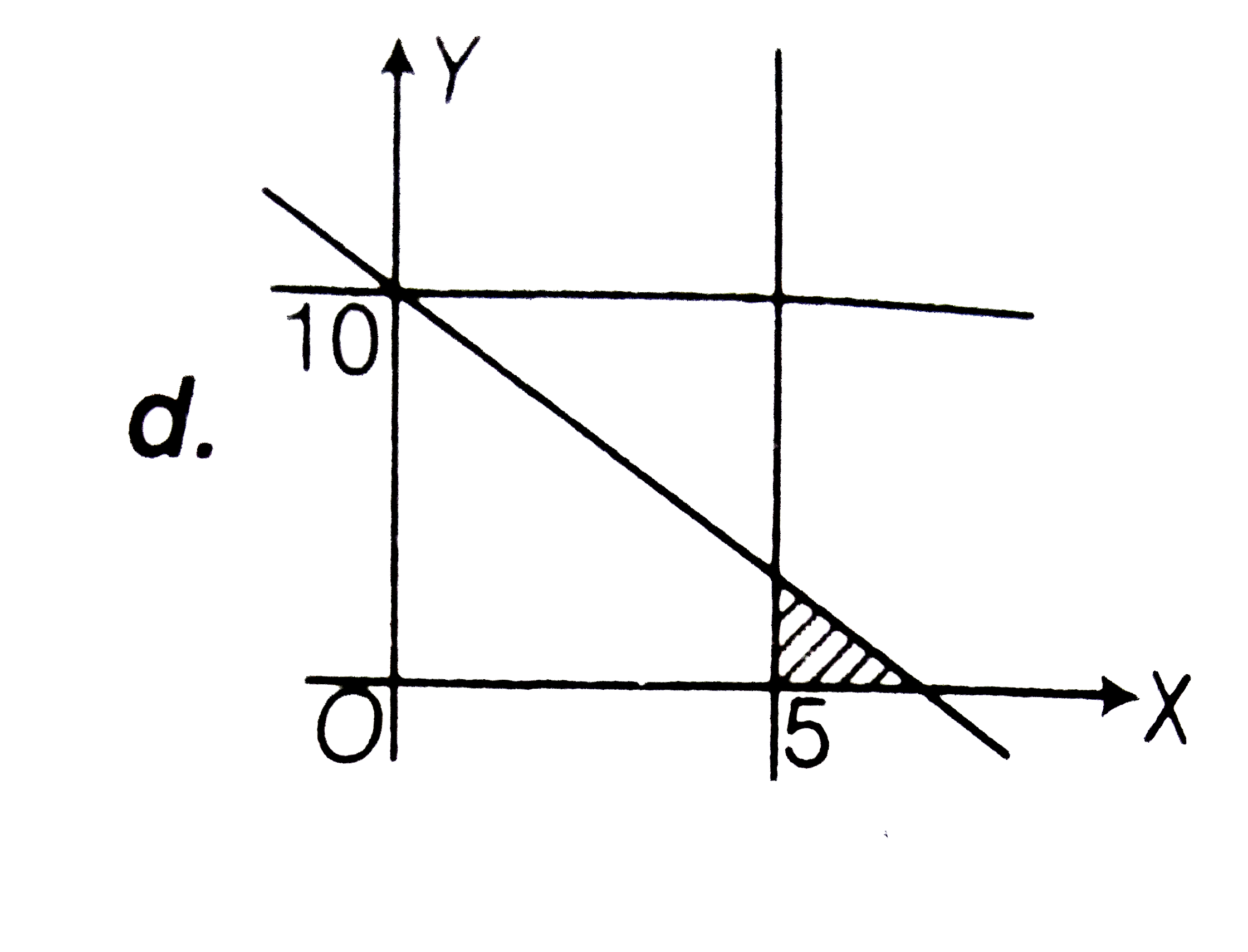
Write the negation of the following statement: All cats scratch.
View SolutionWrite the negation of the statement :p: There exist a number x such that 0<x<1 is ____________________.
View SolutionWrite the negation of the following statement: All birds sing:
View SolutionWrite the negation of the following statement: All primes are odd.
View SolutionIdentify the quantifier in the following statements and write the negation of the statements.
For every real number x,x is less than x+1.
View Solution
