A body is projected horizontally with a velocity of $10 m s^{- 1}$ from the top of building 20 m high. Find
(a) horizontal distance from the bottom of the building at which the body will strike the ground.
(b) the magnitude and direction of the velocity of the body 1s after it is projected. Take $g = 10 m s^{- 2}$ .

Text Solution

Verified by Experts

(a) Refer figure.

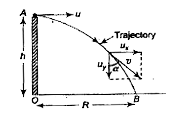
Given $h = - 20 m, u = 10 m s^{- 1}, and g = - 10 m s^{- 2}$ . Time taken by the body to go from A to B is
$t = \sqrt{\frac{2 h}{g}} = \sqrt{\frac{2 \times - 20}{- 10}} = 2 s$
Horizontal distance OR=R=ut= $10 \times 2 = 20$ m
(b) Refer to figure again. horizontal velocity at $t = 1 s$ is $υ_{x} = u = 10 m s^{- 1}$ . vertical velocity at t=1 s is (since initial vertical component of velocity $u_{y} = 0$ )
$υ_{y} = u_{y} + a t = 0 - 10 \times 1 \Rightarrow υ_{y} = - 10 m s^{- 1}$
Magnitude of resultant velocity is $υ = \sqrt{υ_{x}^{2} + υ_{y}^{2}} = \sqrt{10^{2} + {(- 10)}^{2}}$
$= \sqrt{200} = 10 \sqrt{2} m s^{- 1}$
The angle $α$ which the resultant velocity vector subtends with the vertical is given by
$\tan α = \frac{υ_{x}}{| υ_{y} |} = \frac{10}{10} = 1 \Rightarrow α = 45^{\circ}$ .

Updated on:21/07/2023

A body is projected horizontally with a velocity of $4 m s^{- 1}$ from the top of a high tower. The velocity of the body after 0.7 is nearly (Take, $g = 10 m s^{- 2})$
A $10 m s^{- 1}$
B $8 m s^{- 1}$
C $19.2 m s^{- 1}$
D $11 m s^{- 1}$
A ball of mass 2 kg is projected horizontally with a velocity 20m/s from a building of height 15m. The speed with which body hits the ground is :
A20 m/s
B $10 {(7)}^{1 / 2} m / s$
C25 m/s
D35 m/s