From on the ground at a distance x from the foot of a pole, a ball is thrown, at an angle of 60∘, which just touch the top of a pole and strikes the ground at a distance of y, on the other side of it. The height of the pole.
√2xy(x+y)
√3xy(x+y)
2xy(x+y)
xyx+y
The correct Answer is:B
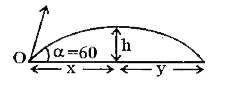
Let .h. be height of the pole, h=xtanα(1−xR)
∴h=xtan60∘(1−x(x+y))=√3xy(x+y)
Similar Questions
From a point on the ground at a distance a from the foot of a pole, a ball is thrown at an angle of 45∘, which just touches the top of the pole and strikes the ground at a distance of b, on the outer side of it. Find the height of the pole.
View SolutionFrom a point on the ground at a distance a from the foot of a pole, a ball is thrown at an angle of 45∘, which just touches the top of the pole and strikes the ground at a distance of b, on the outer side of it. Find the height of the pole.
View Solution
Knowledge Check
From a point on the ground at a distance of 2m from the fot of a verticle wal, a ball is thrown at an angle of 45∘ which just clears the top of the wall and then strikes the ground at distance of 4m from the foot of the wall on the other side. The height of the wall is
A3mB2/3mC3/4mD4/3mA body is projected at an angle of 45∘ with horizontal from a point on ground at distance 6m from the foot of a vertical pole. It just crosses the top of the pole and falls on ground on the other side at a distance of 3m from the foot of the pole. The height of the pole is:
A1mB2mC3mD4mA ball projected from ground at an angle of 45∘ just clears a wall infront. If point of projection is 4m from the foot of wall and ball strikes the ground at a distance of 6m on the other side of the wall, the height of the wall is
A4.4mB2.4mC3.6mD1.6m
From a pint on the ground at a distance 15m from the foot of a vertical wall, a ball is thrown at an angle of 45∘ which just clears the top of the wall and afterwards strikes the ground at a distance 5m on the other side. Find the height of the wall.
View SolutionA vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60∘ and the angle of depression of the bottom of the tower is 30∘ . Find :
the height of the pole, if the height of the tower is 75 m
View SolutionA vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60∘ and the angle of depression of the bottom of the tower is 30∘ . Find :
the height of the tower, it the height of the pole is 20 m ,
View SolutionA ball is projectedfrom ground at an angle 45∘ with horizontal from distance d1 from the foot of a pole and just after touching the top of pole it the falls on ground at distance d2 from pole on other side, the height of pole is
View SolutionA ball is projected from at an angle 45∘ with horizontal from distance d1 from the foot of a pole and just after touching the top of pole it the falls on ground at distance d2 from pole on other side, the height of pole is
View Solution
