If the perimeter of a rectangle is 24 units and the length exceeds the breadth by 4 units, then find the area of a rectangle .
The correct Answer is:32 square units
To solve the problem step by step, we will use the information provided about the perimeter and the relationship between the length and breadth of the rectangle.
Step 1: Understand the given information
We know that:
- The perimeter of the rectangle is 24 units.
- The length (L) exceeds the breadth (B) by 4 units.
Step 2: Write the formula for the perimeter of a rectangle
The formula for the perimeter (P) of a rectangle is given by:
P=2(L+B)
Step 3: Set up the equation using the perimeter
Since the perimeter is 24 units, we can write:
2(L+B)=24
Step 4: Simplify the perimeter equation
Dividing both sides of the equation by 2 gives us:
L+B=12
This is our first equation.
Step 5: Express length in terms of breadth
We are also given that the length exceeds the breadth by 4 units:
L=B+4
This is our second equation.
Step 6: Substitute the expression for L into the first equation
Now, we can substitute the expression for L from the second equation into the first equation:
(B+4)+B=12
Step 7: Combine like terms
Combining the terms gives us:
2B+4=12
Step 8: Solve for B
Subtract 4 from both sides:
2B=12−4
2B=8
Now, divide by 2:
B=4
Step 9: Find the length using the value of breadth
Now that we have the breadth, we can find the length using the second equation:
L=B+4=4+4=8
Step 10: Calculate the area of the rectangle
The area (A) of a rectangle is given by:
A=L×B
Substituting the values of L and B:
A=8×4=32
Final Answer
The area of the rectangle is 32 square units.
---
We know that:
- The perimeter of the rectangle is 24 units.
- The length (L) exceeds the breadth (B) by 4 units.
The formula for the perimeter (P) of a rectangle is given by:
P=2(L+B)
Since the perimeter is 24 units, we can write:
2(L+B)=24
Dividing both sides of the equation by 2 gives us:
L+B=12
This is our first equation.
We are also given that the length exceeds the breadth by 4 units:
L=B+4
This is our second equation.
Now, we can substitute the expression for L from the second equation into the first equation:
(B+4)+B=12
Combining the terms gives us:
2B+4=12
Subtract 4 from both sides:
2B=12−4
2B=8
Now, divide by 2:
B=4
Now that we have the breadth, we can find the length using the second equation:
L=B+4=4+4=8
The area (A) of a rectangle is given by:
A=L×B
Substituting the values of L and B:
A=8×4=32
The area of the rectangle is 32 square units.
Topper's Solved these Questions
- POLYNOMIALSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - POLYNOMIALSEXERCISE - EXERCISE (Subjective problems (Long answer type))
5 Videos
- POLYNOMIALSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - POLYNOMIALSEXERCISE - EXERCISE (Integral /numerical value type)
10 Videos
- POLYNOMIALSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - POLYNOMIALSEXERCISE - EXERCISE (Subjective problems (Very short answer type))
9 Videos
- NUMBER SYSTEMSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - NUMBER SYSTEMSEXERCISE - Olympiad/HOTS Corner
20 Videos
- PROBABILITYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
Similar Questions
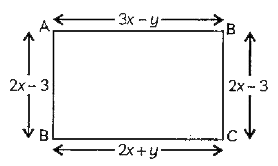
Given that the perimeter of the rectangle is 120cm, find:
the length and the breadth
View SolutionIf the length of a rectangle is reduced by 5 units and its breadth is increased by 2 units then the area of the rectangle is reduced by 80 sq units. However, if we increase its length by 10 units and decrease the breadth by 5 units, its area increased by 50 sq units. Find the length and breadth of the rectangle.
View Solution
Knowledge Check
If the length and breadth of a rectangle are in the ratio 13: 8 and its perimeter is 420 m, then find the area of the rectangle.
A12000m2B9400m2C1040m2DSquareThe difference between the length and the breadth of a rectangle is 7 Cms and the perimeter of the rectangle is 50 Cms What is the area of the rectangle ?
A144 Sq CmsB154 Sq CmsC288 Sq CmsD216 Sq CmsArea of a rectangle =L×B
Perimeter of a rectangle = 2(L + B) where L and B are the length and breadth of the rectangle respectively.
The area of a rectangle whose length 20 cm and breadth 15 cm isA105cm2B300cm2C35cm2D30cm2
The perimeter of a rectangle is 40 m. Its length is four metres less than five times its breadth. Find the area of the rectangle.
View SolutionFind the perimeter of the rectangle, if its length is 5 times of a and breadth is 3 units.
View SolutionThe perimeter of a rectangle is 130 cm. If the breadth of the rectangle is30 cm, find its length. Also find the area of the rectangle.
View SolutionIf the area of rectangle is 24 sq. cm and the length and breadth are integers in cm, then find the maximum possible perimeter of the rectangle.
View SolutionThe breadth of a rectangle is 3 less than the length.if both length and breadth are reduced by 3 units,the area of the rectangle reduces by 176 sq.units.find the dimensions of the original rectangle
View Solution
