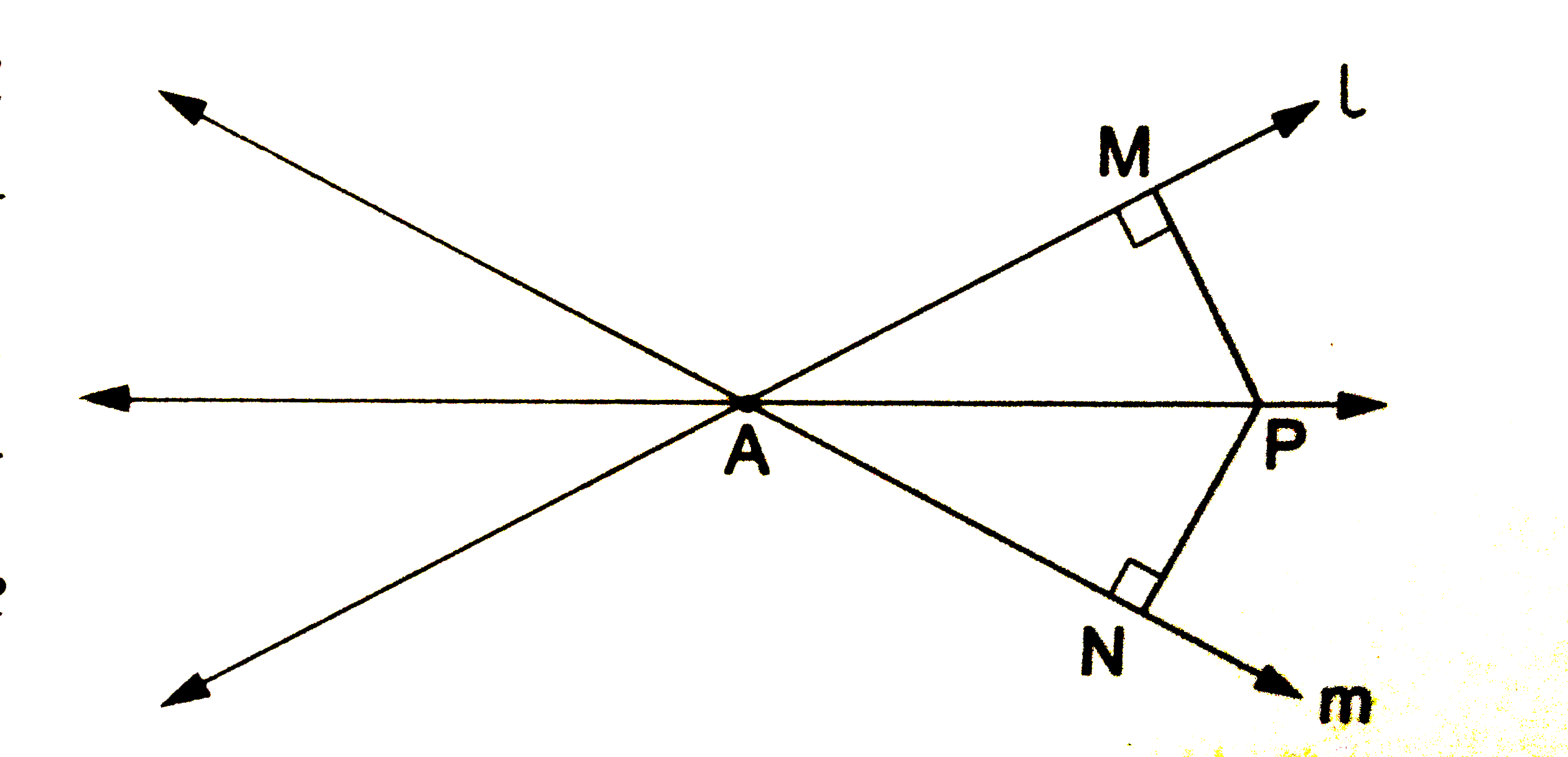
In figure P is a point equidistant from the lines l and m intersecting at point A. Show that the line n (along AP) bisects the angle between l and m.

Step by step video & image solution for In figure P is a point equidistant from the lines l and m intersecting at point A. Show that the line n (along AP) bisects the angle between l and m. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
P is a point equidistant from two lines l and m intersecting at point A(see Fig. 7.38). Show that the line AP bisects the angle between them.
View SolutionP is a point equidistant from two lines l and m intersecting at a point A see in figure, Show that AP bisects the angle between them. Figure
View Solution
Knowledge Check
The loucs of a point which is a equidistant from two non-intersecting lines l and m is a _____
Astraight line parallel to the line lBStraight line parallel to the line mCStraight line parallel to the line l and m and midway between themDstraight line that intersects both the line l and m
P is a point equidistant from two lines l and m intersecting at a point A, as shown in the given figure. Show that the line AP bisects tha angle between them.
View SolutionThe locus of a point equidistant from two intersecting lines is
View SolutionShow that the locus of a point, equidistant from two intersecting lines in the plane, is a pair of lines bisecting the angles formed by the given lines.
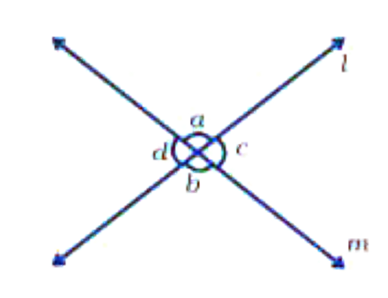
View SolutionIn Fig. 5.12, lines l and m intersect each other at a point. Which of the following is false?
View SolutionShow that the locus of a point, equidistant from two intersecting lines in the plane, is a pair of lines bisecting the angles formed by the given lines.
View SolutionProve that the locus of the point equidistant from two given points is the straight line which bisects the line segment joining the given points at right angles.
View Solutionl and m are intersecting lines, lllp and mllq, find the relation between p and q.
View Solution
