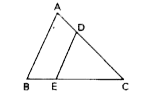
In figure, it is given that AE=AD and BD=CE. Prove that ΔAEB≅ΔADC.
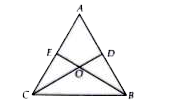
Step by step video & image solution for In figure, it is given that AE=AD and BD=CE. Prove that DeltaAEB~=DeltaADC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.1)
14 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.2)
9 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - OLYMPAID/ HOTS CORNER
10 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
In Figure, it is given that AE=AD and BD=CE. Prove that AEB ≅ADC
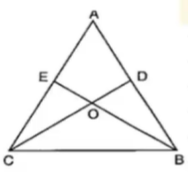
View SolutionIn the given figure, AB = AC and AD = AE. Prove that:
ΔABD≅ΔACE
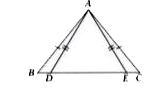
View SolutionIn Figure, it is given that AB=EF, BC=DE, AB ⊥BD and FE ⊥CE. Prove that ABD ≅FEC.
View SolutionIn the given figure, AB = AD and ∠1=∠2. Prove that : ΔABC≅ΔADC

View SolutionIn the figure, if ∠A=∠B and AD=BE. Prove that CD = CE.
View SolutionIn the given figure, ∠1=∠2andACBD=CBCE prove that ΔACB~ΔDCE.

View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
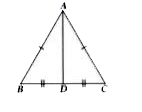 Prove that:
Prove that:
ΔADB≅ΔADC
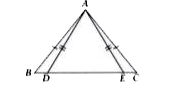
View SolutionIn the given figure, AB = AC and AD = AE. Prove that:
BD = CE
View SolutionIn the given figure, in ΔABC,∠B=∠CandBD=CE. Prove that DE∣∣BC.

View SolutionIn the figure, AD is the bisector of angle BAC. Prove that AB>BD.
View Solution
