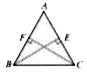
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Step by step video & image solution for BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.4)
6 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.5)
4 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.2)
9 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
If the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
View SolutionIf the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
In△ABEand △ACF∠AEB=∠AFC(900each)
∠BAE=∠CAF(common angle)
∠ABE=∠ACF using angle sum property
BE=CF,△ABE≅△ACF
⇒AB=AC
Hence triangle ABC is an isosceles tangent as two sides are equal to each other
View Solution
Knowledge Check
BE and CF are two altitudes of a triangle ABC. If AB=6cm,AC=5cmand CF=4cm, then the length of BE is
A4.8 cmB7.5 cmC3.33 cmD5.5 cmIf AD, BE, CF are the altitudes of ΔABC whose orthocentre is H, then C is the orthocentre of :
A△ABHB△BDHC△ABDD△BEA
In a triangle ABC, if ∠A=∠B+∠C, the prove that triangle ABC is a right triangle.
View SolutionIf in a ΔABC,c(a+b)cosB/2=b(a+c)cosC/2, prove that the triangle is isosceles.
View SolutionIn △ABC, if cosA+sinA−2cosB+sinB=0 then prove that triangle is isosceles right angled.
View SolutionIn figure, AD and BE are respectively altitudes of an isosceles triangle ABC with AC=BC . Prove that AE=BD.
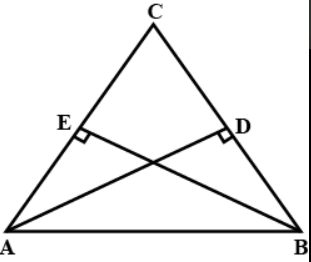
View SolutionIn a ΔABC if (a+b)cos(B2)=b(a+c)cos(C2) then prove that the triangle ABC is isosceles.
View SolutionIf AD, BE, CF are the altitudes of triangle ABC whose ortho centre is H then C is ortho centre of
View Solution
