Question

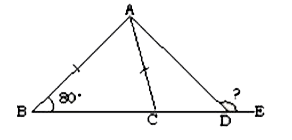
In ${\displaystyle \Delta ABC}$ if ${\displaystyle AB=AC\text{and}\angle B={70}^{\circ }}$, then ${\displaystyle \angle C=2a^{\circ }}$. Find the value of a

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the properties of the triangle
Given that triangle ABC has sides AB and AC equal, we can conclude that triangle ABC is an isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are also equal.

Step 2: Identify the angles
We are given:
- \( AB = AC \)
- \( \angle B = 70^\circ \)

Let \( \angle A = \angle C = x \) (since \( AB = AC \), the angles opposite these sides are equal).

Step 3: Use the triangle sum property
The sum of the angles in any triangle is \( 180^\circ \). Therefore, we can write the equation:
\( \angle A + \angle B + \angle C = 180^\circ \)
Substituting the known values:
\( x + 70^\circ + x = 180^\circ \)
This simplifies to:
\( 2x + 70^\circ = 180^\circ \)

Step 4: Solve for \( x \)
Now, we will isolate \( x \):
\( 2x = 180^\circ - 70^\circ \)
\( 2x = 110^\circ \)
\( x = \frac{110^\circ}{2} = 55^\circ \)

Step 5: Relate \( x \) to \( a \)
We know from the problem statement that \( \angle C = 2a^\circ \). Since we found \( \angle C = x = 55^\circ \), we can set up the equation:
\( 2a = 55^\circ \)

Step 6: Solve for \( a \)
Now we can solve for \( a \):
\( a = \frac{55^\circ}{2} = 27.5^\circ \)

Conclusion
Thus, the value of \( a \) is \( 27.5^\circ \).

---