ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse ABand parallel to BC intersects AC at D. Show that(i) D is the mid-point of AC (ii) MD⊥AC(iii) CM = MA=12AB
Step by step video & image solution for ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse ABand parallel to BC intersects AC at D. Show that(i) D is the mid-point of AC (ii) M D_|_A C(iii) C M\ =\ M A=1/2A B by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-1 )
35 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-2 )
15 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - NCERT SECTION (Exercise 8.1 )
20 Videos
- PROBABILITYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
ABC is a triangle right-angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD⊥AC
(iii) CM = MA=12AB
View SolutionABC is a triangle right-angled at C. A line through the midpoint P of hypotenuse AB and parallel to BC intersects AC at M. Show that
(i) M is the midpoint of AC,
(ii) MP⊥AC,
(iii) CP=AP=12AB.
View Solution
Knowledge Check
In the figure, ABC is a triangle in which AB=AC. A circle through B touches AC at D and intersects AB at P. If D is the mid - point of AC, Find the value of AB :
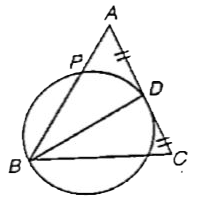 A2APB3APC4APD4√2cm
A2APB3APC4APD4√2cmIf ABC is a right angled triangle at B and M, N are the mid-points of AB and BC, then 4(AN2+CM2) is equal to :
A4AC2B6AC2C5AC2D54AC2△ABC is a right angled at A and AD is the altitude to BC. If AB= 7 cm and AC = 24 cm. Find the ratio of AD is to AM if M is the mid-point of BC.
A25:41B32:41C336/625D625/336
ΔABC is a right triangle right angled at A such that AB=AC and bisector of ∠C intersects the side AB at D. Prove that AC+AD=BC.
View SolutionABC is a triangle right angled at B. D is a point on AC such that ∠ABD=45∘ If AC=6 and AD=2 then AB=
View SolutionIn Fig. 3, ABC is a right triangle, right angled at C and D is the mid-point of BC. Prove that AB2=4AD2−3AC2.
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.

View SolutionABC is a right angled triangle. B being the right angle. Mid-points of BC and AC are respectively B' and A'. Area of ΔA'B'C' is
View Solution
