Draw a rough figure and label suitably in each of the following cases:
XY and PQ intersect at M
To solve the problem of drawing a rough figure where lines XY and PQ intersect at point M, follow these steps:
1. Draw Line XY: Start by drawing a straight line on your paper. This will represent line XY. You can draw it horizontally or diagonally, as the orientation does not affect the solution.
Hint: Remember that a line extends infinitely in both directions, so you can draw it longer than the area you need.
2. Label Line XY: Once you have drawn the line, label it as XY. You can write this label above or below the line.
Hint: Make sure the label is clear and distinct so that it can be easily identified.
3. Draw Line PQ: Next, draw another straight line that intersects the first line XY. This will represent line PQ. You can draw it vertically or at an angle to ensure it crosses line XY.
Hint: The intersection point should be clearly visible, so try to make sure the lines cross each other.
4. Label Line PQ: After drawing the second line, label it as PQ. Similar to the first line, place this label above or below the line.
Hint: Keep the labeling consistent in style with the first line for clarity.
5. Mark the Intersection Point M: Identify the point where lines XY and PQ intersect. This point is called M. Mark this point clearly and label it as M.
Hint: Use a small dot or a circle to indicate the intersection point, making it stand out.
6. Final Review: Review your figure to ensure that both lines are clearly labeled and that the intersection point M is marked correctly.
Hint: Double-check that the lines intersect at the point M and that all labels are legible.
Final Figure Description:
You should now have a rough figure showing two lines, XY and PQ, intersecting at point M. The lines should be clearly labeled, and the intersection point should be marked distinctly.
You should now have a rough figure showing two lines, XY and PQ, intersecting at point M. The lines should be clearly labeled, and the intersection point should be marked distinctly.
Topper's Solved these Questions
- BASIC GEOMETRICAL IDEASBOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - NCERT SECTION(EXERCISE 4.2)
10 Videos
- BASIC GEOMETRICAL IDEASBOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - NCERT SECTION(EXERCISE 4.3)
9 Videos
- BASIC GEOMETRICAL IDEASBOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - SOLVED EXAMPLES
36 Videos
- ALGEBRABOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- DATA HANDLING BOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLING EXERCISE - Olympiad/HOTS Corner
10 Videos
Similar Questions
Draw a rough figure and label suitably in each of the following cases:
¯¯¯OP and ¯¯¯OQ meet at O
View SolutionDraw a rough figure and label suitably in each of the following cases:
Points P lies on ¯¯¯AB
View SolutionDraw a rough figure and label suitably in each of the following cases:
Line l contains E and F but not D
View SolutionDraw a rough figure and label suitably in each of the following cases:
(a) Point p lies on AB.
(b) XY and PQ intersect at M.
(c) Line I contains E and F but not D.
(d) OP r and OQ meet at O
View SolutionDraw the lines of symmetry in each of the following figures.

View SolutionDraw the line (or lines) of symmetry of each of the following figures.
View SolutionDraw all lines of symmetry for each of the following figures :
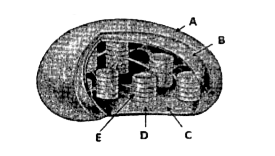
View SolutionLabel the parts in the following figure.

View SolutionLabel the parts in the following figure.
View SolutionDraw a ray diagram in each of the following cases to show the formation of image, when the object is placed :
anywhere in front of a concave lens.
View Solution
