The diameter of a circle passes through___
The centre
The circumference
Any where in the interior
Always two points
The correct Answer is:a
To solve the question "The diameter of a circle passes through___", we can follow these steps:
1. Understand the Definition of Diameter:
- The diameter of a circle is a straight line segment that passes through the center of the circle and connects two points on its boundary (circumference).
Hint: Remember that the diameter is the longest chord of the circle.
2. Identify the Components of the Circle:
- A circle consists of a center point (let's call it O) and a boundary. The diameter will have two endpoints on this boundary.
Hint: Visualize the circle and identify its center and boundary.
3. Draw the Diameter:
- If you draw a line segment from one point on the boundary of the circle, through the center O, to another point on the opposite side of the boundary, you have created the diameter.
Hint: Ensure that the line segment touches the circle at both ends.
4. Conclude the Answer:
- Since the diameter passes through the center of the circle, we can conclude that the diameter of a circle passes through the center.
Hint: Think about the definition of the center of a circle and its relationship to the diameter.
Final Answer:
The diameter of a circle passes through the center.
- The diameter of a circle is a straight line segment that passes through the center of the circle and connects two points on its boundary (circumference).
- A circle consists of a center point (let's call it O) and a boundary. The diameter will have two endpoints on this boundary.
- If you draw a line segment from one point on the boundary of the circle, through the center O, to another point on the opposite side of the boundary, you have created the diameter.
- Since the diameter passes through the center of the circle, we can conclude that the diameter of a circle passes through the center.
The diameter of a circle passes through the center.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - EXERCISE(MCQ)LEVEL-210videos
BASIC GEOMETRICAL IDEAS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - MATCH THE FOLLOWING2videos
BASIC GEOMETRICAL IDEAS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - NCERT SECTION(EXERCISE 4.6)20videos
BASIC GEOMETRICAL IDEAS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - OLYMPIAD/HOTS CORNER20videos
ALGEBRA
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLING EXERCISE - Olympiad/HOTS Corner10videos
DATA HANDLING
Similar Questions
Fill in the blanks: The diameter of a circle is … times its radius The diameter of a circle is the … chord of the circle. The diameter of a circle pass through…. A chord of a circle is a line segment with its end points on the … If we join any two points on a circle by a line segment, we obtain… A radius of a circle is a line segment with one end at …. and the other end at…. All radii of a circle are… The diameters of circle are… The total number of diameters of circle is… Every point on a circle is…from its centre.. A chord of a circle contains exactly….points of the circle.. A diameter is the longest… Concentric circles are circle having….
View SolutionIf the lines x+y=6andx+2y=4 are diameters of the circle which passes through the point (2, 6), then find its equation.
View Solution
Knowledge Check
- Question 1 - Select One
The length of the diameter of the circle which passes through the point (2,3) and touches the x-axis at the point (1,0) is
A53B65C103D35 - Question 2 - Select One
If (h,k) is the centre of a circle passing through the origin then its equation is
Ax2+y2−hx−ky=0Bx2+y2+hx−ky=0Cx2+y2+2hx+2ky=0Dx2+y2−2hx−2ky=0
The radius of the circle x2+y2−2x+3y+k=0 is 212. Find the value of k. Find also the equation of diameter of the circle which passes through the point (5,212).
View SolutionThe diameters of a circle are along 2x+y−7=0andx+3y−11=0.Then the equation of this circle, whichalso passes through (5, 7) is
View SolutionThe diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure (Fig 11.12) AB is a diameter of the circle; C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).
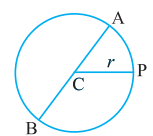 View Solution
View SolutionThe diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure, AB is a diameter of the circle, C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).
 View Solution
View SolutionThe equation of the circle passing through the point (1,1)
View SolutionThe radius of the circle passing through the vertices of the triangle ABC, is
View Solution

