are congruent in any correspondence. PQ = 5 cm, PR = 4 cm and . If LM = 5 cm and QR = MN, then LN equals
3 cm
5 cm
4 cm
can't be determined
The correct Answer is:C
To solve the problem, we will use the properties of congruent triangles. Given that triangles ΔPRQ and ΔLMN are congruent, we can establish the relationships between their corresponding sides and angles.
1. Identify Given Values:
- PQ=5cm
- PR=4cm
- ∠P=30∘
- LM=5cm
- QR=MN
2. Use Congruence of Triangles:
Since ΔPRQ is congruent to ΔLMN, we can match their corresponding sides and angles. The congruence can be represented as:
- PQ corresponds to LM
- PR corresponds to LN
- QR corresponds to MN
3. Set Up Corresponding Sides:
From the congruence:
- PQ=LM
- PR=LN
- QR=MN
4. Substitute Known Values:
- We know PQ=5cm and LM=5cm (this is given).
- We also know PR=4cm.
5. Find LN:
Since PR corresponds to LN and PR=4cm, it follows that:
LN=PR=4cm
6. Conclusion:
Therefore, the length of LN is 4cm.
Final Answer:
LN=4cm
- PQ=5cm
- PR=4cm
- ∠P=30∘
- LM=5cm
- QR=MN
Since ΔPRQ is congruent to ΔLMN, we can match their corresponding sides and angles. The congruence can be represented as:
- PQ corresponds to LM
- PR corresponds to LN
- QR corresponds to MN
From the congruence:
- PQ=LM
- PR=LN
- QR=MN
- We know PQ=5cm and LM=5cm (this is given).
- We also know PR=4cm.
Since PR corresponds to LN and PR=4cm, it follows that:
LN=PR=4cm
Therefore, the length of LN is 4cm.
LN=4cm
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Match the following
2 Videos
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Assertion & Reaction Type
5 Videos
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - NCERT Section (Exercise 7.2)
20 Videos
- COMPARING QUANTITIES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - COMPARING QUANTITIES EXERCISE - Olympaid/HOTS Corner
20 Videos
- DATA HANDLINGBOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLINGEXERCISE - Olympiad / Hots Corner
20 Videos
Similar Questions
Knowledge Check
If ΔPQRand ΔLMN are similar and 3PQ=LMandMN=9cm, then QR is equal to :
A12 cmB6 cmC9 cmD3 cmIn a triangle PQR, PQ = 20 cm and PR = 6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of theseIn a triangle PQR, PQ=20 cm and PR =6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of the above
Construct △PQR in which QR=3.4cm, ∠P=50∘ and PQ−PR=1.2cm.
View SolutionConstruct a parallelogram PQRS, when PQ=3.7cm,QR=2.3cm,andPR=4.8cm.

View Solution
In the figure given above, ∠PQR=90∘ and QL is a median, PQ=5cmandQR=12cm, Then QL is equal to:
View SolutionConstruct a △PQR in which PQ=5.3 cm. PR = 4.6 cm and QR = 3.8 cm.
View SolutionIn the figure given below, ∠PQR=90∘andQL is a median, PQ=5cmandQR=12cm. Then QL is equal to
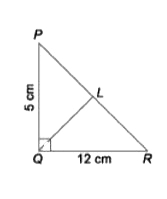
View Solution
