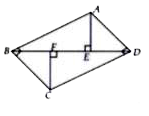
CF and AE are equal perpendiculars on BD, BF = FE = ED angleBAE=

CF and AE are equal perpendiculars on BD, BF = FE = ED

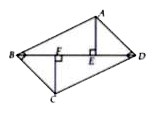
ABCD is a
ARectangle
BSquare
CRhombus
DKite
CF and AE are equal perpendiculars on BD, BF = FE = ED

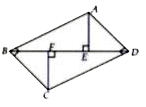
$Δ A B E$ is congruent to
A $Δ A E D$
B $Δ B F C$
C $Δ C D F$
D $Δ B C D$
Chords AB and CD of a circle interest at E and are perpendicular to each other. Segments AE, EB and ED are of lengths 2 cm, 6 cm and 3 cm respectively. Then the length of the diameter the circle in cm is :
A $\sqrt{65}$
B $\frac{1}{2} \sqrt{65}$
C $65$
D $\frac{65}{2}$

CF and AE are equal perpendiculars on BD, BF = FE = ED

$∠ B A E =$ ____.