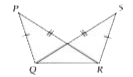
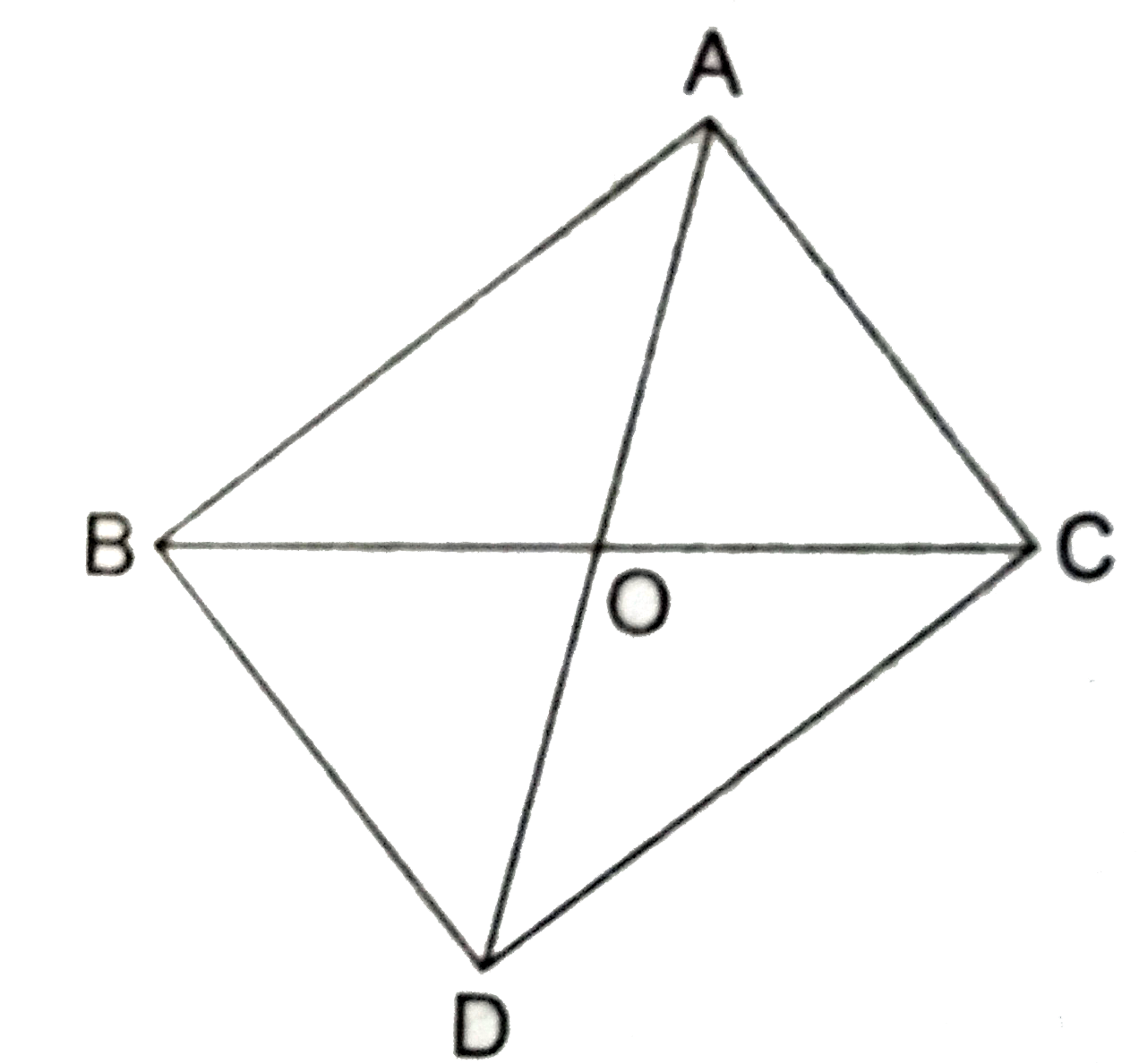
In the given figure, we have AO = BO and CO = DO. Prove that ΔAOC≅ΔBOD.

Step by step video & image solution for In the given figure, we have AO = BO and CO = DO. Prove that DeltaAOC~=DeltaBOD. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Subjective Problems (Short Answer Type)12videos
CONGRUENCE OF TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Subjective Problems (Long Answer Type)10videos
CONGRUENCE OF TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Comprehension Type6videos
CONGRUENCE OF TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - COMPARING QUANTITIES EXERCISE - Olympaid/HOTS Corner20videos
COMPARING QUANTITIES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLINGEXERCISE - Olympiad / Hots Corner20videos
DATA HANDLING
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, If AB and CD bisect each other at O, then ΔAOC is congruent to
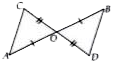 AΔBODBΔDOBCΔDOBDΔBDO
AΔBODBΔDOBCΔDOBDΔBDO
In the given figure, we have PQ = SR and Pr = SQ. Prove that:

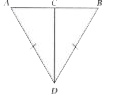
∠PQR=∠SRQView SolutionIn the given figure, we have C is the mid-point of AB and DA = DB.
Prove that : ∠DCA=∠DCB.
 View Solution
View SolutionIn the given figure, AB=AC. prove that :
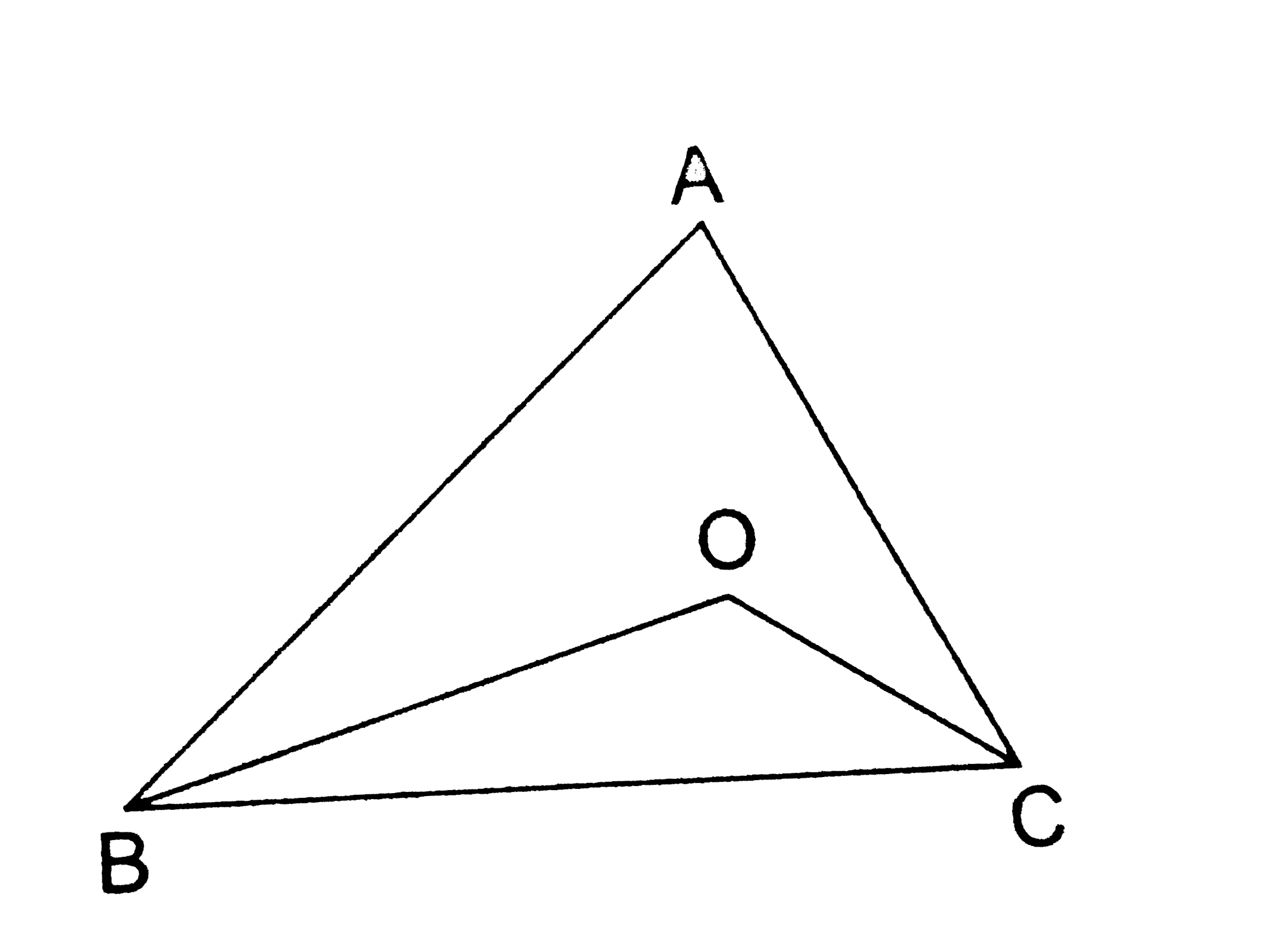
View SolutionIn the given figure, Oa = OB and OC = OD. Which is the criteria to prove
ΔAOC≅ΔBOD.
 View Solution
View SolutionIn the given figure we have ∠1=∠3and∠2=∠4 show that ∠A=∠C
View SolutionIn the given figure, AB>AC. If BO and CO are the bisectors of ∠Band∠C respectively then
 View Solution
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
 View Solution
View Solution