In two triangles PQR and LMN, PQ = QR, ∠P=∠MandQR=LN, then which of the following is true?
Triangles are congruent only
Triangles are isosceles only
Triangles are both congruent and isosceles
can't be determined
The correct Answer is:D
To solve the problem, we need to analyze the information given about the two triangles, PQR and LMN, and determine the relationship between them based on the properties of congruence.
1. Identify the Given Information:
- We have two triangles: PQR and LMN.
- The following conditions are provided:
- PQ = QR (This indicates that triangle PQR is isosceles with sides PQ and QR being equal).
- ∠P = ∠M (Angle P in triangle PQR is equal to angle M in triangle LMN).
- QR = LN (This indicates that side QR in triangle PQR is equal to side LN in triangle LMN).
2. Understanding Triangle Properties:
- Since PQ = QR, triangle PQR is isosceles.
- The property of isosceles triangles states that the angles opposite to the equal sides are also equal. Therefore, if PQ = QR, then ∠Q = ∠R.
3. Analyzing the Angles:
- We know that ∠P = ∠M.
- Since ∠Q and ∠R are equal (because triangle PQR is isosceles), we can denote them as ∠Q = ∠R = x.
- The sum of angles in triangle PQR is 180 degrees, so:
- ∠P + ∠Q + ∠R = 180
- ∠M + x + x = 180
- ∠M + 2x = 180
4. Comparing the Triangles:
- We have established that triangle PQR has two equal angles (due to it being isosceles) and one angle equal to angle M in triangle LMN.
- However, we do not have enough information about the sides of triangle LMN or the other angles in triangle LMN to definitively conclude that the two triangles are congruent.
5. Conclusion:
- Since we cannot establish that the two triangles are congruent based on the given information, we conclude that we cannot determine the relationship between the two triangles definitively.
- Therefore, the correct answer is: Triangles can't be determined.
- We have two triangles: PQR and LMN.
- The following conditions are provided:
- PQ = QR (This indicates that triangle PQR is isosceles with sides PQ and QR being equal).
- ∠P = ∠M (Angle P in triangle PQR is equal to angle M in triangle LMN).
- QR = LN (This indicates that side QR in triangle PQR is equal to side LN in triangle LMN).
- Since PQ = QR, triangle PQR is isosceles.
- The property of isosceles triangles states that the angles opposite to the equal sides are also equal. Therefore, if PQ = QR, then ∠Q = ∠R.
- We know that ∠P = ∠M.
- Since ∠Q and ∠R are equal (because triangle PQR is isosceles), we can denote them as ∠Q = ∠R = x.
- The sum of angles in triangle PQR is 180 degrees, so:
- ∠P + ∠Q + ∠R = 180
- ∠M + x + x = 180
- ∠M + 2x = 180
- We have established that triangle PQR has two equal angles (due to it being isosceles) and one angle equal to angle M in triangle LMN.
- However, we do not have enough information about the sides of triangle LMN or the other angles in triangle LMN to definitively conclude that the two triangles are congruent.
- Since we cannot establish that the two triangles are congruent based on the given information, we conclude that we cannot determine the relationship between the two triangles definitively.
- Therefore, the correct answer is: Triangles can't be determined.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Subjective Problems (Long Answer Type)
10 Videos
- COMPARING QUANTITIES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - COMPARING QUANTITIES EXERCISE - Olympaid/HOTS Corner
20 Videos
- DATA HANDLINGBOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLINGEXERCISE - Olympiad / Hots Corner
20 Videos
Similar Questions
Knowledge Check
In the figure, in triangles PQR and TQR , PQ = TR and PR = TQ . Which of the following statements is true ?
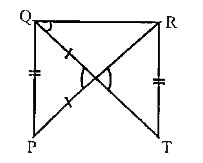 AΔPQR≅ΔTRQBΔPQR≅ΔTQRCΔPQR≅ΔPQTDΔPQR≅ΔQTR
AΔPQR≅ΔTRQBΔPQR≅ΔTQRCΔPQR≅ΔPQTDΔPQR≅ΔQTRIf in two triangles ABC and PQR, ABQR=BCPR , then which of the following is true?
AΔBCA~ΔPQRBΔPQR~ΔCABCΔPQR~ΔABCDΔCBA~ΔPORΔPQRandΔTQR are on the same base QR and on the same side of QR . If PQ = TR and PR = TQ, then which of the following is correct ?
AΔPQR≅ΔTQRBΔPQR≅ΔTRQCΔPQR≅ΔRQRDΔPQR≅ΔQTR
In ΔPQR,PQ=4 cm, PR = 6 cm and QR = 3 cm . Which of the following is correct ?
View SolutionIn ΔPQR,PQ=4cm,PR=6cmandQR=3cm. Which of the following is correct?
View SolutionIn ΔPQR,PQ=4cm,PR=6cmandQR=3cm. Which of the following is correct?
View SolutionIn the figure, in ΔPQRandΔTQR,PQ=TRandPR=TQ. Which of the following statements is true?
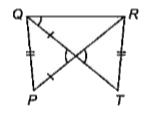
View SolutionIn a triangle PQR, let ∠PQR=30∘ and the sides PQ and QR have lengths 10√3 and 10, respectively. Then, which of the following statement(s) is (are) TRUE ?
View Solution
