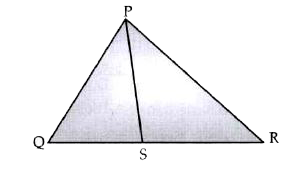
In the figure , PS is the bisector of ∠QPR of ΔPQR . Prove that QSSR=PQPR .

The correct Answer is:=PQPR
Topper's Solved these Questions
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise: Exercise (Multiple Choice Questions) (LEVEL -1 )
Explore 35 Videos
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise: Exercise (Multiple Choice Questions) (LEVEL -2)
Explore 15 Videos
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise:NCERT Section Exercise 6.5
Explore 21 Videos
- SURFACE AREAS AND VOLUMESBook:MTG IIT JEE FOUNDATIONChapter:SURFACE AREAS AND VOLUMESExercise:OLYMPIAD/HOTS CORNER
Explore 20 Videos
Similar Questions
In the figure given below PS is the bisector of ∠QPR of ΔPQR . Prove that QSSR=PQPR .
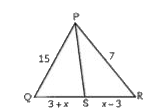
View SolutionIn the given figure, PS is the bisector of ∠QPR . If PO = 15, PR = 7, QS = 3 + x and SR = x - 3, find the value of x.
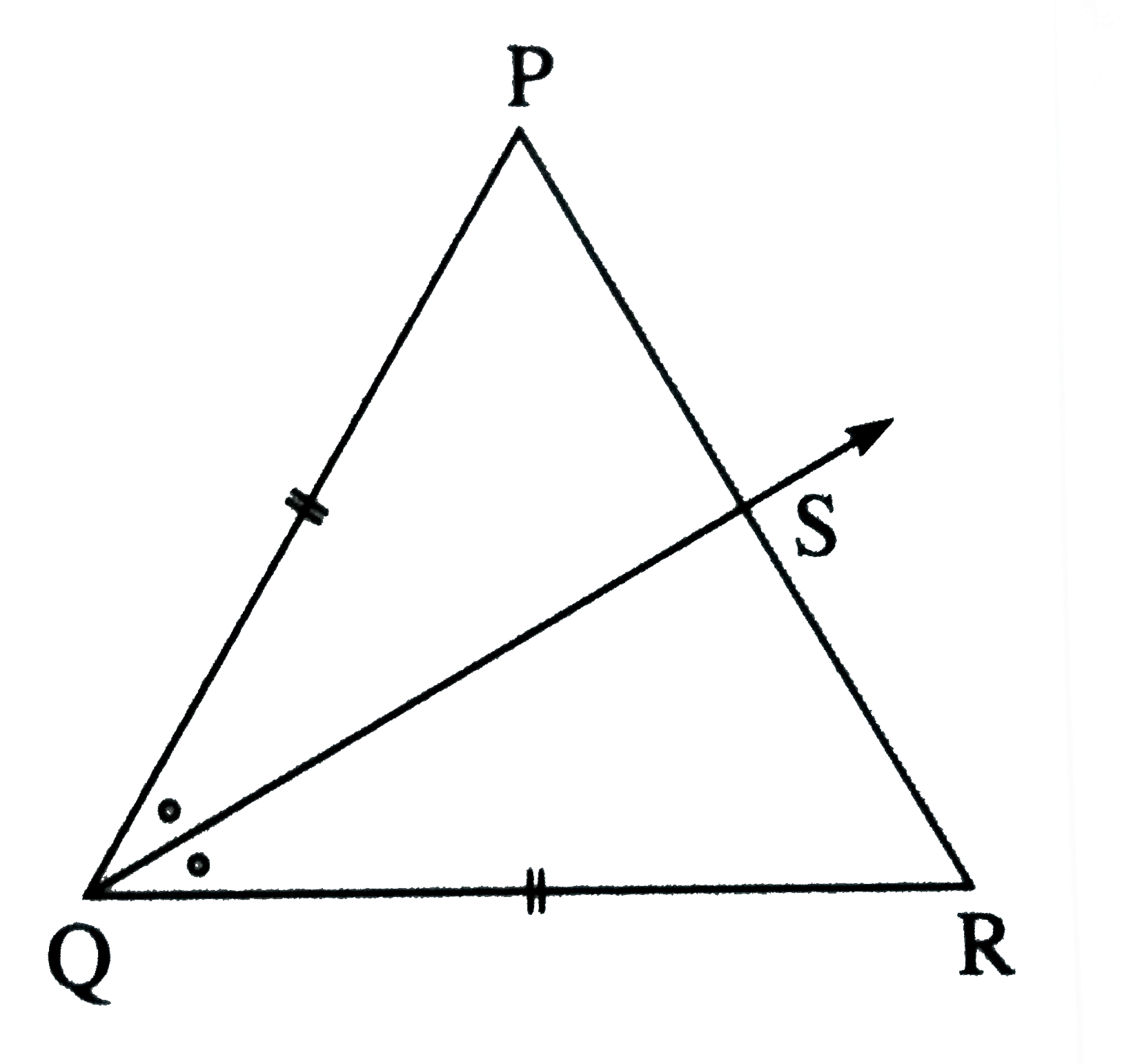
View SolutionIn the figure, ray QS is the bisector of ∠PQR and PQ=QR.
Then PSSR=………..
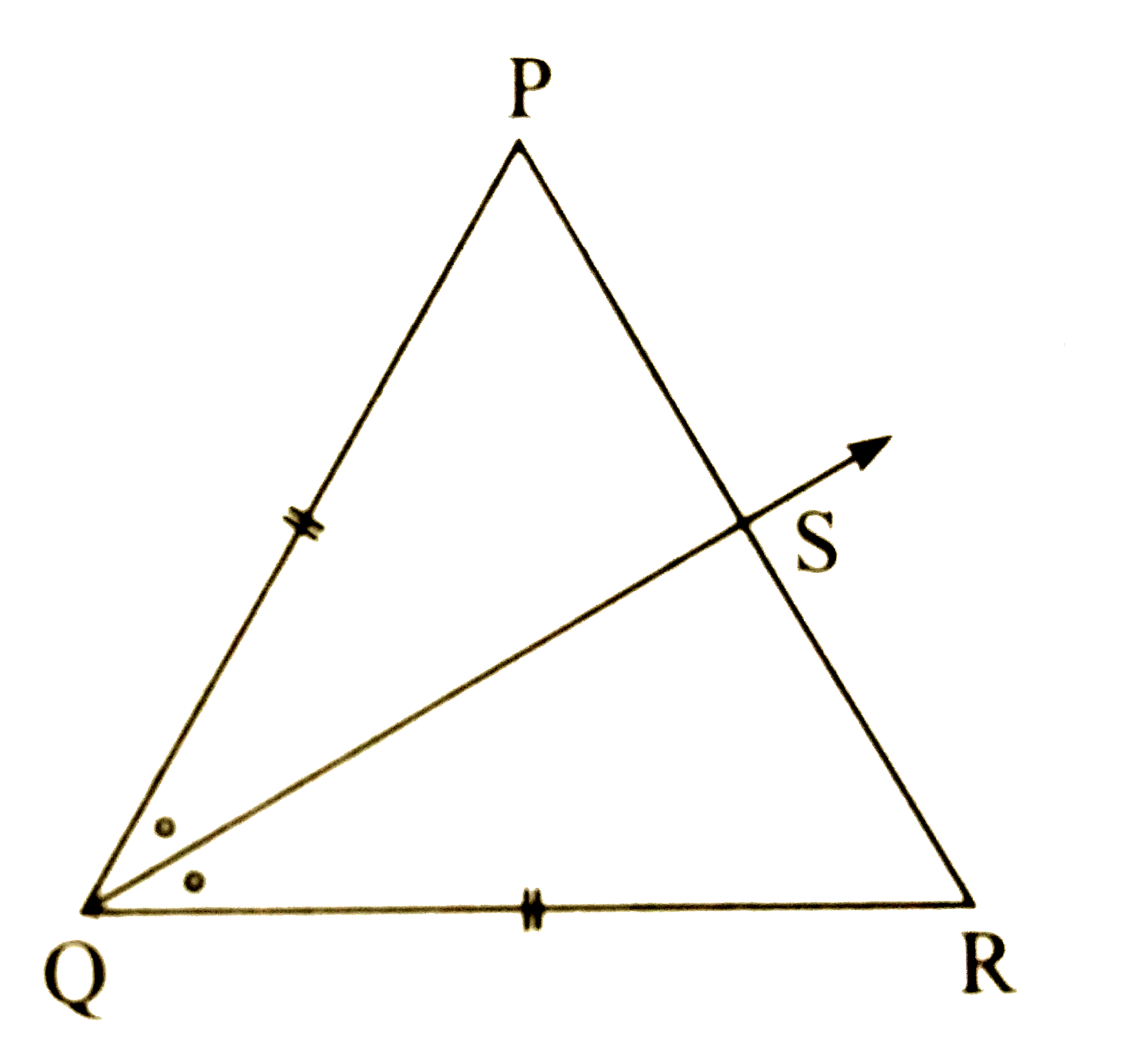
View SolutionIn the figure ray QS is the bisector of ∠PQR and PQ=QR, then PSSR=………..
View SolutionIn the given figure, Q is a point on the side SR of ΔPSR such that PQ = PR. Prove that PS>PQ.
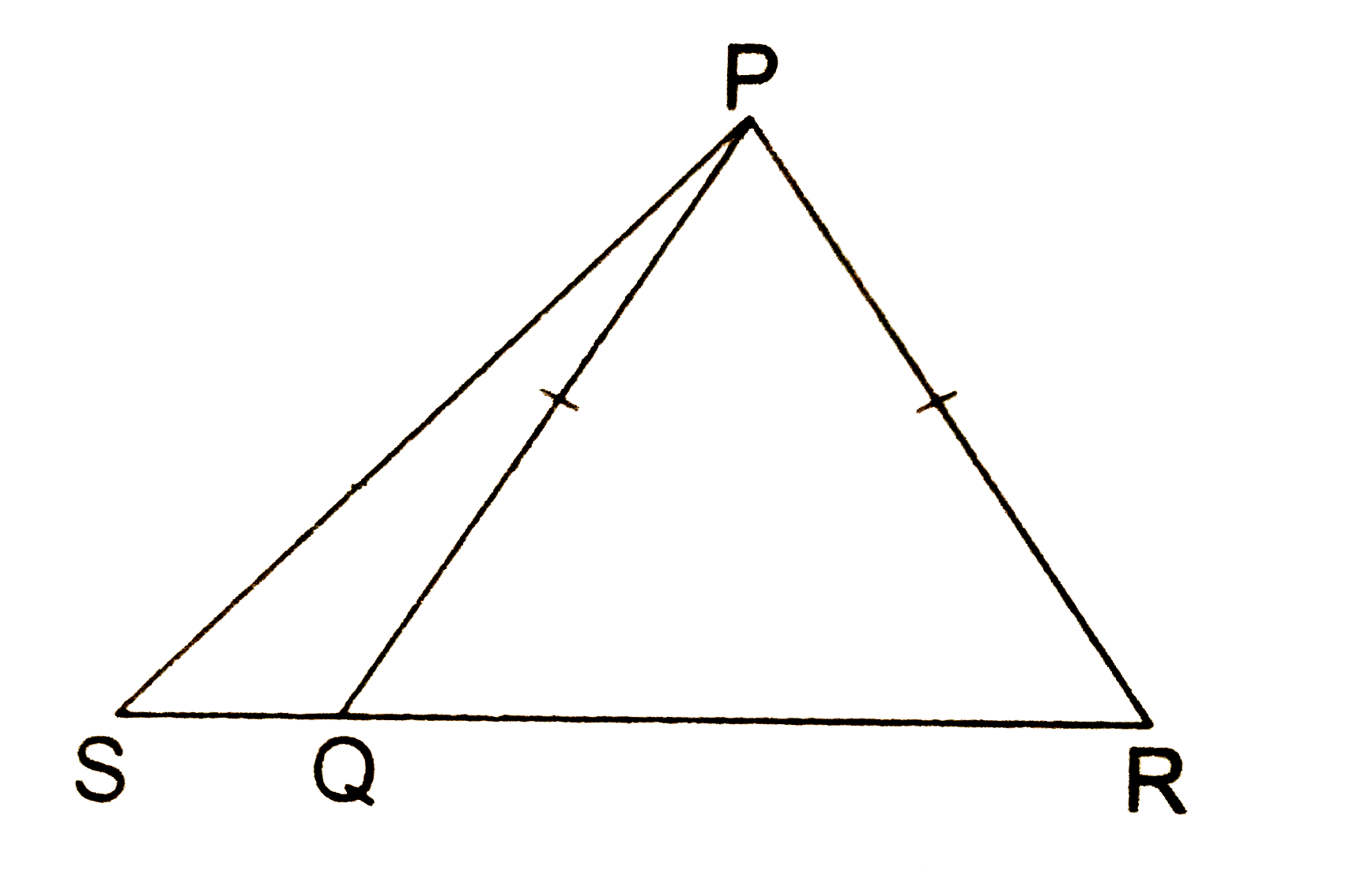
View SolutionIn the given figure, PS=PR,∠TPS=∠QPR. Prove that PT=PQ.
View SolutionIn △PQR, PS is the internal bisector of ∠P meeting QR at S, PQ =16cm, PR = 22.4 cm and QR = 9.6cm. The length of SR(in cm) is:
△PQR में, PS, ∠P , का आंतरिक द्विभाजक है जो QR से S पर मिलता है l यदि PQ = 16cm, PR = 22.4 cm और QR = 9.6 cm तो SR (सेमी में) की लंबाई है
View SolutionPQR is a triangle, whose area is 180 cm2. S is a point on side QR, such that PS is the angle bisector of ∠QPR. If PQ: PR = 2: 3, then what is the area (in cm2) triangle PSR?
View SolutionIn the figure 2.35,ΔPQR is an equilatral triangle. Point S is on seg QR such that QS=13QR. Prove that : 9PS2=7PQ2
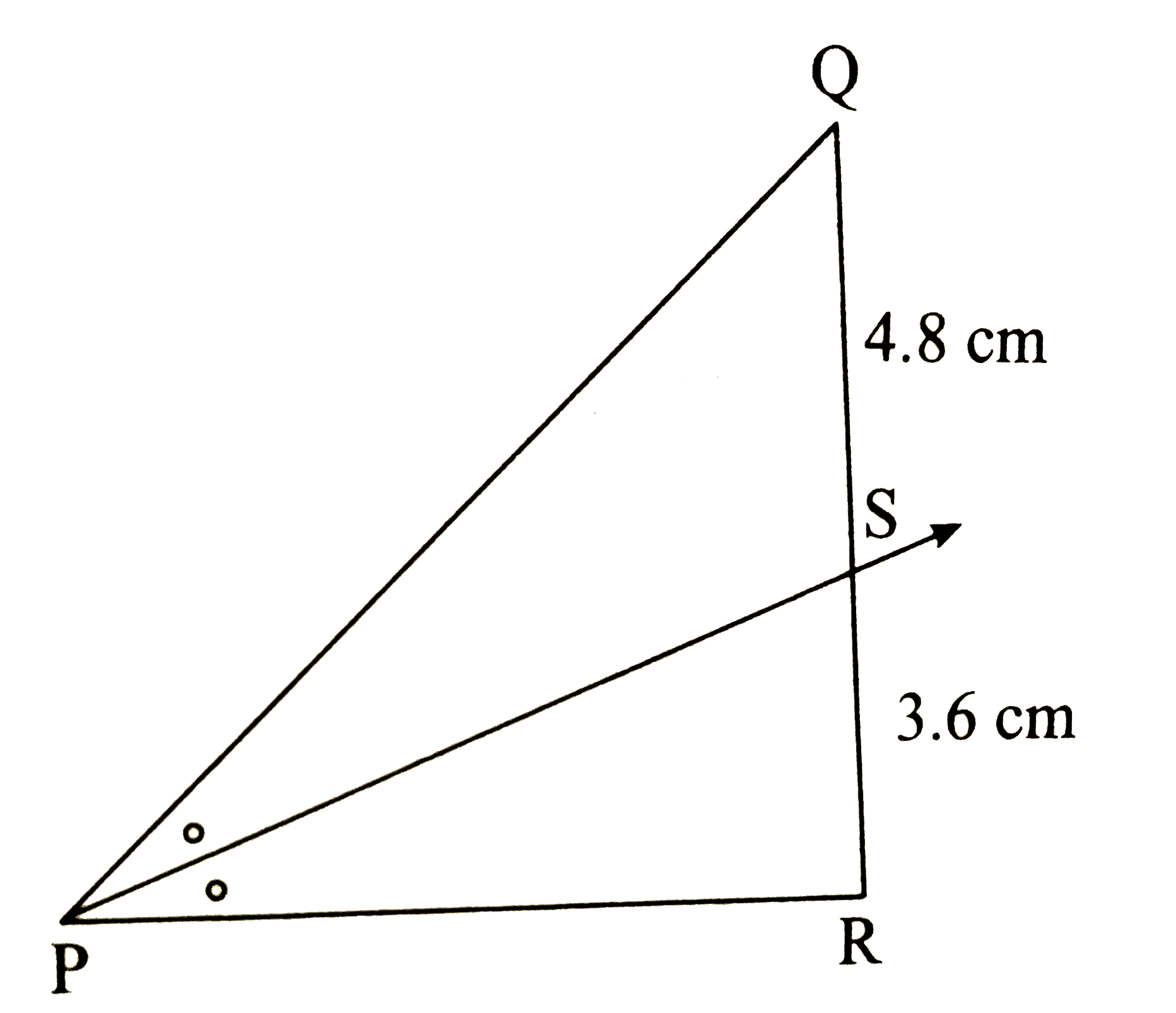
View SolutionIn ΔPQR, ray PS is the bisector of ∠QPR, Q−S−R. If Qs=4.8cm, SR=3.6cm, find PQ:PR.
View Solution
