Equal forces F act on isolated bodies A and B as shown in figure. The mass of B is three times that of A. The magnitude of the acceleration of A is:
three times that of B
1/3 that of B
nine times that of B
1/9 that of B
The correct Answer is:A
To solve the problem, we need to apply Newton's second law of motion, which states that the force acting on an object is equal to the mass of the object multiplied by its acceleration (F = ma).
1. Identify the Forces and Masses:
- Let the mass of body A be mA.
- Since the mass of body B is three times that of A, we have mB=3mA.
2. Apply Newton’s Second Law:
- For body A, the force acting on it is F, and according to Newton's second law:
F=mA⋅aA(Equation 1)
- For body B, the force acting on it is also F:
F=mB⋅aB(Equation 2)
3. Substitute the Mass of B:
- Substitute mB=3mA into Equation 2:
F=3mA⋅aB
4. Set the Two Equations Equal:
- Since both equations equal F, we can set them equal to each other:
mA⋅aA=3mA⋅aB
5. Cancel mA from Both Sides:
- Assuming mA≠0, we can divide both sides by mA:
aA=3aB
6. Conclusion:
- The magnitude of the acceleration of A is three times that of B:
aA=3⋅aB
Final Answer:
The magnitude of the acceleration of A is 3 times that of B.
---
- Let the mass of body A be mA.
- Since the mass of body B is three times that of A, we have mB=3mA.
- For body A, the force acting on it is F, and according to Newton's second law:
F=mA⋅aA(Equation 1)
- For body B, the force acting on it is also F:
F=mB⋅aB(Equation 2)
- Substitute mB=3mA into Equation 2:
F=3mA⋅aB
- Since both equations equal F, we can set them equal to each other:
mA⋅aA=3mA⋅aB
- Assuming mA≠0, we can divide both sides by mA:
aA=3aB
- The magnitude of the acceleration of A is three times that of B:
aA=3⋅aB
The magnitude of the acceleration of A is 3 times that of B.
Topper's Solved these Questions
- FORCE AND PRESSURE BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND PRESSURE EXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS LEVEL-2)
22 Videos
- FORCE AND PRESSURE BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND PRESSURE EXERCISE - EXERCISE (MATCH THE FOLLOWING)
1 Videos
- FORCE AND PRESSURE BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND PRESSURE EXERCISE - NCERT SECTION
19 Videos
- FOOTSTEPS TOWARDS NEETBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS NEETEXERCISE - MCQ
45 Videos
- FRICTION BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FRICTION EXERCISE - OLYMPIAD/HOTS CORNER
15 Videos
Similar Questions
Two forces of equal magnitude F act on two isolated bodies P and Q as shown in the figure. The mass of body Q is three times that of body P. The magnitude of the acceleration of P is

View SolutionTwo masses A and B, each of mass M are fixed together by a massless spring. A force acts on the mass B as shown in figure. If the mass A starts moving away from mass B with acceleration 'a', then the acceleration of mass B wil be :-

View Solution
Knowledge Check
Two forces, each equal to F, act as shown in figure. Their resultant is
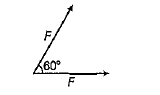 AF/2BFC√3D√5F
AF/2BFC√3D√5FThe velocity - time graph for two bodies A and B are shown in figure. Then, the acceleration of A and B are in the ratio
 Asin25∘ to sin50∘Btan25∘ to tan40∘Ccos25∘ to cos50∘Dtan25∘ to tan50∘
Asin25∘ to sin50∘Btan25∘ to tan40∘Ccos25∘ to cos50∘Dtan25∘ to tan50∘Two forces, each equal to F, act as shown in (figure) Their resultant is
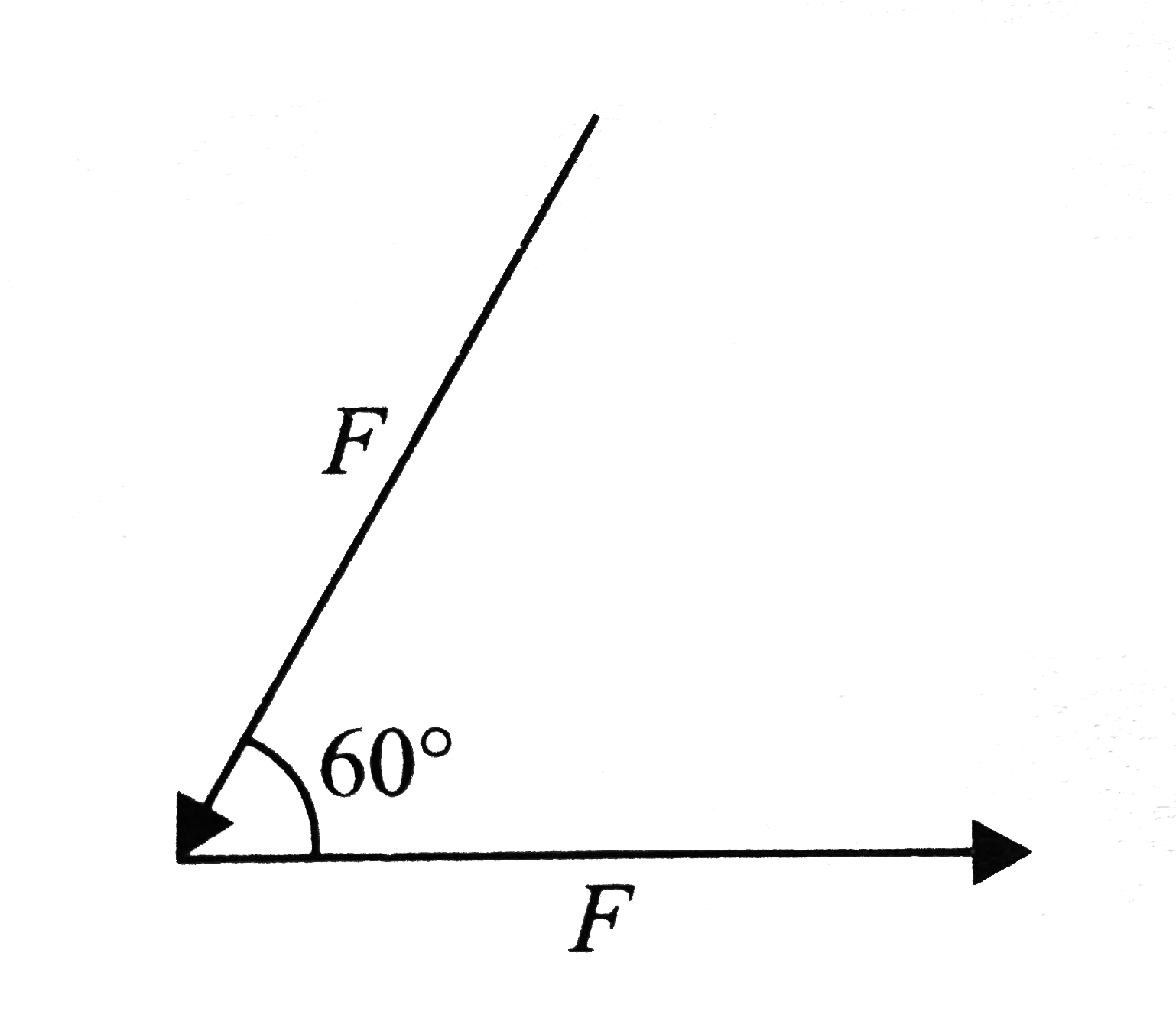 AF/2BFC√3FD√5F
AF/2BFC√3FD√5F
A force F is acted on a body as shown in the figure. Find the impulse of the force in first four seconds.

View SolutionTwo bodies A and B each of mass m are fixed together by a massless spring . A force F acts on the mass B as shown in fig .3 (a)18. At the instant shown , the body A has an acceleration a What is the acceleration of B ?

View SolutionTwo bodies A and B each of mass M are fixed together by a massless spring A force F acts on the mass B as shown in fig At the instant shown the mass A has acceleration a. What is the acceleration of mass B?

View SolutionThree forces are acting on a particle as shown in the figure. To have the resultant force only along the Y-direction, the magnitude of the minimum additional force needed is
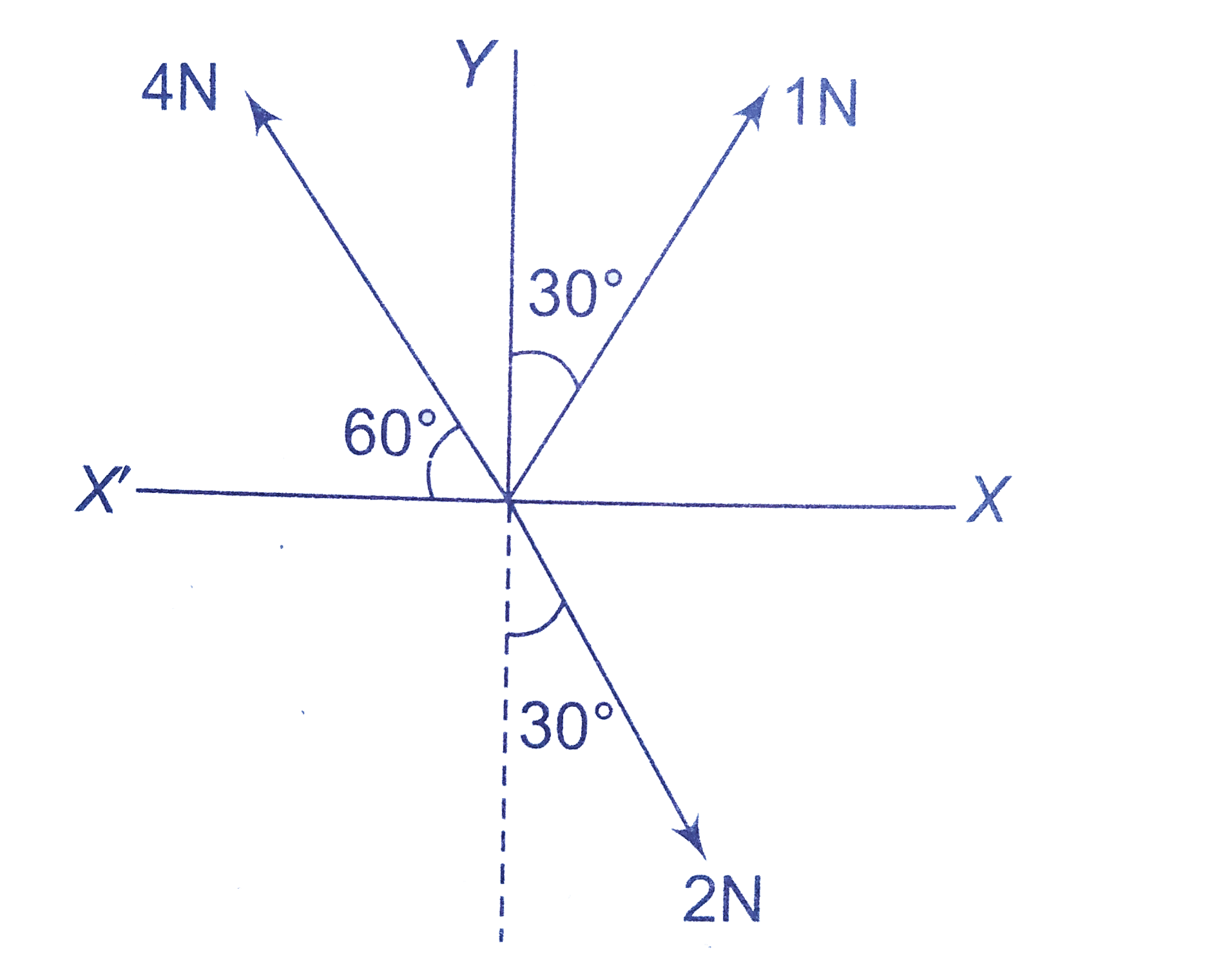
View SolutionTwo blocks of masses M1 and M2 are connected to each other through a light spring as shown in figure. If we push mass M1 with force F and cause acceleration a1 in mass M1. What will be the magnitude of accleration in M2?

View Solution
