Question

A particle is moving in a circle of radius 2 m. Show the following position of the particle.
2 m from the centre, ${30}^{\circ }$ west-north.

Explanation

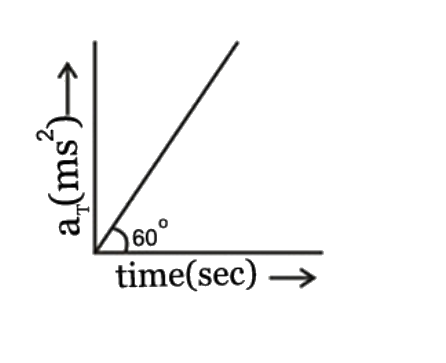
To show the position of a particle moving in a circle of radius 2 m, located at 2 m from the center at an angle of 30 degrees west of north, we can follow these steps:

1. Draw the Circle: Start by drawing a circle with a radius of 2 meters. This represents the path of the particle.

2. Identify the Center: Mark the center of the circle. This point is crucial as it is the reference point for measuring the radius.

3. Draw the Radius: From the center, draw a line that measures 2 meters outward. This line represents the radius of the circle.

4. Determine the Directions: Identify the cardinal directions: North (N) is up, South (S) is down, East (E) is to the right, and West (W) is to the left.

5. Locate the Angle: Since the position is specified as 30 degrees west of north, start from the North direction and measure 30 degrees towards the West.

6. Draw the Angle: From the North direction, draw a line that makes a 30-degree angle towards the West. This line represents the direction of the particle.

7. Mark the Position: The intersection of the 2-meter radius line and the 30-degree west of north line is the position of the particle. Mark this point as Point A.

8. Label the Diagram: Clearly label the center of the circle, the radius, the angle, and the position of the particle (Point A).

Final Diagram:
You should have a circle with a radius of 2 meters, the center marked, the angle of 30 degrees west of north drawn, and the position of the particle indicated at Point A.

---