Calculate the total pressure at the bottom of a lake of depth 5.1 m (atm pressure P), density of water
To calculate the total pressure at the bottom of a lake of depth 5.1 m, we will use the formula for pressure at a certain depth in a fluid, which is given by:
P=P0+ρgh
Where:
- P is the total pressure at depth,
- P0 is the atmospheric pressure,
- ρ is the density of the fluid (water in this case),
- g is the acceleration due to gravity,
- h is the depth of the fluid.
Step 1: Identify the given values
- Atmospheric pressure, P0=105 Pa
- Density of water, ρ=103 kg/m³
- Acceleration due to gravity, g=10 m/s²
- Depth of the lake, h=5.1 m
Step 2: Calculate the pressure due to the water column
Using the formula ρgh:
ρgh=(103kg/m3)×(10m/s2)×(5.1m)
Calculating this gives:
ρgh=103×10×5.1=103×51=5.1×104Pa
Step 3: Calculate the total pressure at the bottom of the lake
Now, we add the atmospheric pressure to the pressure due to the water column:
P=P0+ρgh
P=105Pa+5.1×104Pa
Converting 105 Pa to the same power of ten:
P=105+0.51×105=(1+0.51)×105=1.51×105Pa
Final Answer
The total pressure at the bottom of the lake at a depth of 5.1 m is:
P=1.51×105Pa
- P is the total pressure at depth,
- P0 is the atmospheric pressure,
- ρ is the density of the fluid (water in this case),
- g is the acceleration due to gravity,
- h is the depth of the fluid.
- Atmospheric pressure, P0=105 Pa
- Density of water, ρ=103 kg/m³
- Acceleration due to gravity, g=10 m/s²
- Depth of the lake, h=5.1 m
Using the formula ρgh:
Now, we add the atmospheric pressure to the pressure due to the water column:
P=105Pa+5.1×104Pa
The total pressure at the bottom of the lake at a depth of 5.1 m is:
Similar Questions
A vessel full of water has a bottom of area 20cm2, top of area 20cm2, height 20 cm and volume half a litre as shown in figure.
(a) find the force exerted by the water on the bottom.

(b) considering the equilibrium of the water, find the resultant force exerted by the sides of the glass vessel on the water. atmospheric pressure =1.0×105N/m2. density of water =1000kg/m3 and g=10m/s2
View SolutionThe pressure acting on a submarine is 3×105 at a certain depth. If the depth is doubled the percentage increase in the pressure acting on the submarine would be :
(Assume that atmospheric pressure is 1×105 Pa density of water is 103kgm−3,g−10ms−2)
View Solution
Knowledge Check
If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Water pressure at the bottomof centre of the box is equal to (atmospheric pressure =105N/m2 density of water =1000kg/m3,g=10m/s2)A1.1MPaB0.11MPaC0.101MPaD0.011MPaWhat is the pressure at the bottom of the ocean at a place where it is 3 km deep ?
[atmospheric pressure =1.01×105Pa, Density of sea water =1030kgm−30]A1.01×105PaB3×105PaC1.01×107PaD3×107PaA body is experiencing an atmospheric pressure of 1.01×105N/m2 on the surface of a pond. The body will experience double of the previous pressure if it is brought to a depth of (given density of pond water =1.03×103kg/m2, g=10m/s2)
A8mB8.6mC9.7mD10.3m
The U-tube acts as a water siphon. The bend in the tube is 1m above the water surface. The tube outlet is 7m below the water surface. The water issues from the bottom of the siphon as a free jet at atmospheric pressure. Determine the speed of the free jet and the minimum absolute pressure of the water in the bend. Given atmospheric pressure =1.01×105N/m2,g=9.8m/s2 and density of water =103kg/m3
 .
.
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
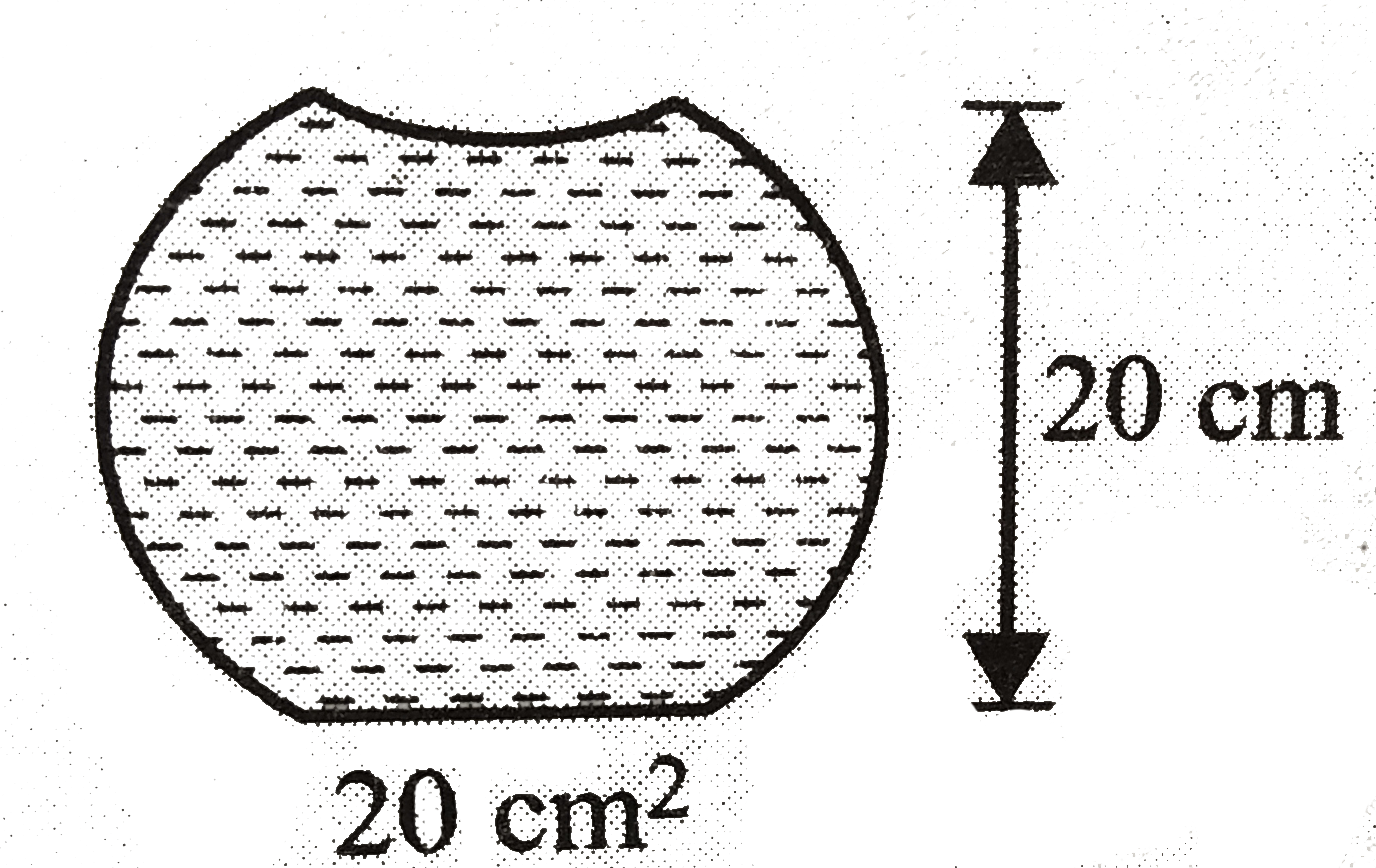
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View SolutionThe pressure at the bottom of a lake due to water is 4.9×106N/m2. What is the depth of the lake?
View SolutionAn experimentally decided formula for relation between pressure and density of x a liquid is
PPatm=(B+1)(ddatm)n−B
B and n are constant. Patm is atmospheric pressure and datm is the density of liquid at that pressure. For water numerical values of B=3000 and n=7.
Take atmospheric pressure=100kPa and density of water =103kg/m3 at atmospheric pressure.
At what depth is the density of water increase by 0.001%.
View SolutionA body is experiencing an atmospheric pressure of 1.01×105N/m2 on the surface of a pound . The body will experience double of the previous pressure if it is brought to a depth of (given density of pound water =1.03×103kg/m2,g=10m/s2 )
View Solution
