A body of weight 50 N is placed on a smooth surface. If the force required to move the body on the surface is 30 N the coefficient of friction
0.60
1.2
0.3
1.67
To find the coefficient of friction (μ) for a body of weight 50 N placed on a smooth surface, where the force required to move the body is 30 N, we can follow these steps:
1. Identify the Given Information:
- Weight of the body (W) = 50 N
- Force required to move the body (F) = 30 N
2. Understand the Concept of Friction:
- The force of friction (f) that opposes the motion is equal to the applied force when the body is just about to move. Therefore, in this case, f = F = 30 N.
3. Use the Formula for Friction:
- The formula for the force of friction is given by:
f=μ×N
where:
- f = force of friction
- μ = coefficient of friction
- N = normal force
4. Determine the Normal Force:
- For a body resting on a horizontal surface, the normal force (N) is equal to the weight of the body. Therefore, N=W=50N.
5. Substitute the Values into the Friction Formula:
- Now, substituting the known values into the friction formula:
30N=μ×50N
6. Solve for the Coefficient of Friction (μ):
- Rearranging the equation to solve for μ:
μ=30N50N
- Simplifying this gives:
μ=0.6
7. Conclusion:
- Therefore, the coefficient of friction (μ) is 0.6.
Final Answer:
The coefficient of friction is 0.6.
---
- Weight of the body (W) = 50 N
- Force required to move the body (F) = 30 N
- The force of friction (f) that opposes the motion is equal to the applied force when the body is just about to move. Therefore, in this case, f = F = 30 N.
- The formula for the force of friction is given by:
f=μ×N
where:
- f = force of friction
- μ = coefficient of friction
- N = normal force
- For a body resting on a horizontal surface, the normal force (N) is equal to the weight of the body. Therefore, N=W=50N.
- Now, substituting the known values into the friction formula:
30N=μ×50N
- Rearranging the equation to solve for μ:
μ=30N50N
- Simplifying this gives:
μ=0.6
- Therefore, the coefficient of friction (μ) is 0.6.
The coefficient of friction is 0.6.
Similar Questions

Three blocks are connected as shown in the figure. Valculate the minimum force required to move the body with constant velocity. The coefficient of friction at all surfaces is 0.25.
View SolutionA weight 'W' rests on a horizontal plane. What will be the least force required to move the body alone the plane,if the angle of friction is 0?
View Solution
Knowledge Check
The force required to move a body up a rough inclined plane is double the force required to prevent the body from sliding down the plane. The coefficient of friction when the angle of inclination of the plane is 60∘ is
A1√2B1√3C12D13The force required to move a body up a rough inclined plane is double the force required to prevent the body from sliding down the plane. The coefficient of friction when the angle of inclination of the plane is 60∘ is .
A1√2B1√3C12D13In the figure, a block of weight 60N is placed on a rough surface. The coefficient of friction between the block and the surface is 0.5 . What should be the weight W such that the block does not slip on the surface?
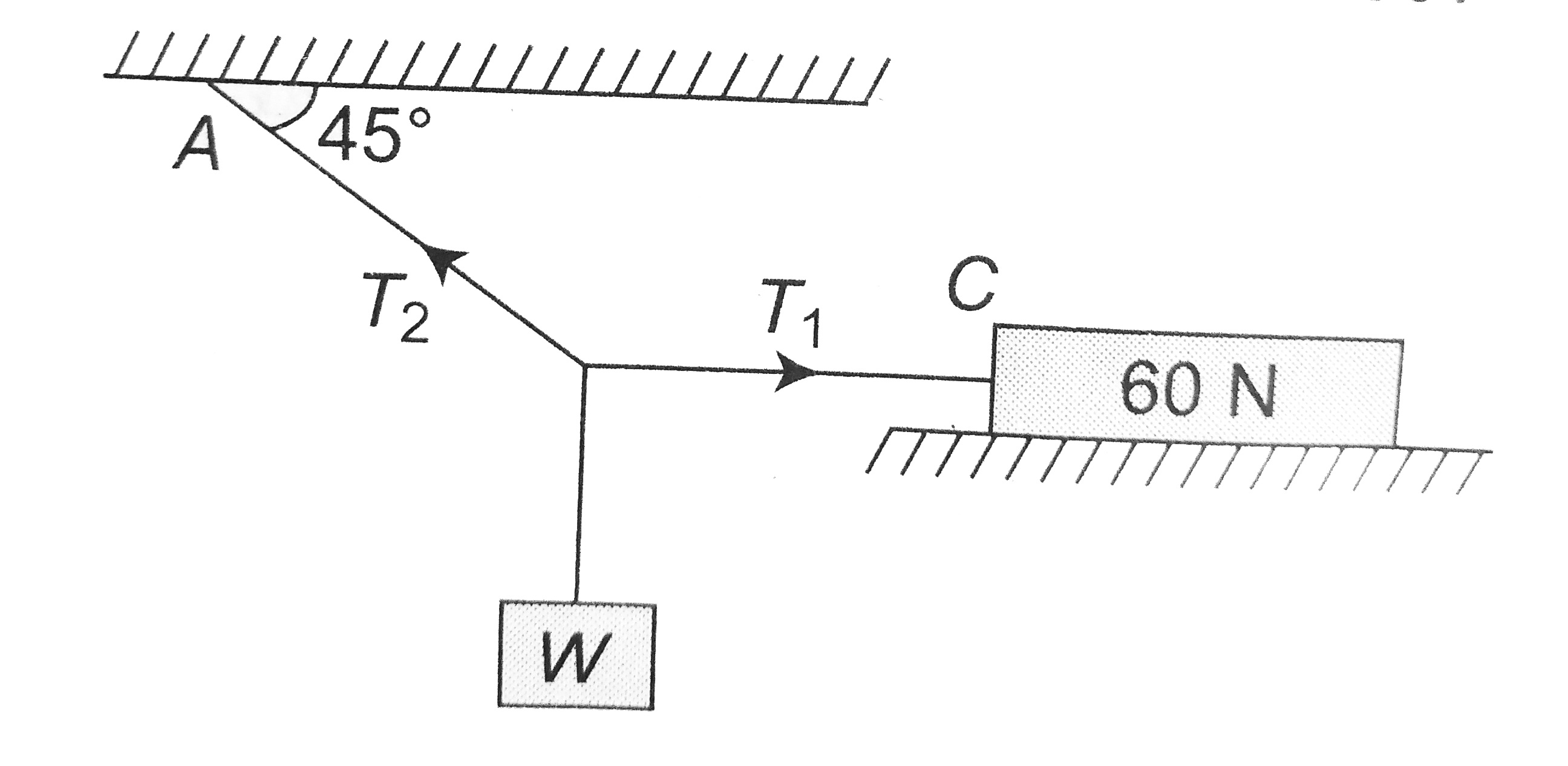 A60NB60√2NC30ND30√2N
A60NB60√2NC30ND30√2N
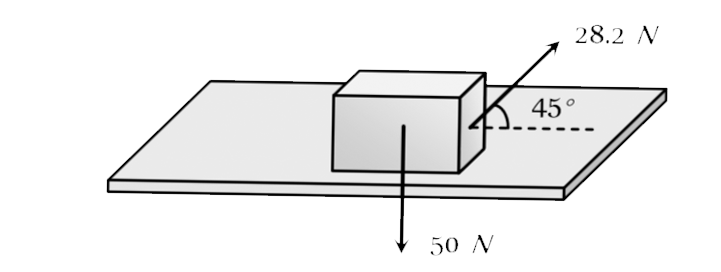
A body of weight 50 N placed on a horizontal surface is just moved by a force of 28.2 N. the frictional force and the narmal reaction are
View SolutionThe force F1 required to just moving a body up an inclined plane is double the force F2 required to just prevent the body from sliding down the plane. The coefficient of friction is μ. The inclination θ of the plane is :
View SolutionA horizontal force of 20 N is applied to a block of 10 kg resting on a rough horizontal surface. How much additional force is required to just move the block, if the coefficient of static friction between the block and the surface is 0.4 ?
View SolutionThe force required just to move a body up an inclined plane is double the force required just to prevent the body sliding down. If the coefficient of friction is 0.25 , the angle of inclination of the plane is
View SolutionA body weight 500 N on the surface of the earth. How much would it weigh half way below the surface of the earth
View Solution
