Derive an expression for electric field intensity at any point due to short dipole ?

Text Solution

Verified by Experts

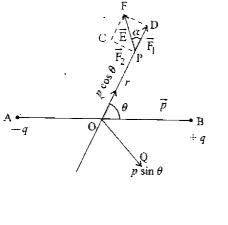
Consider a short electric dipole AB having dipole moment $\to p$ . Let P be the point at a distance r from the centre O. Let the line OP of the dipole makes an angle $θ$ with the direction of dipole moment $\to P$ .
Resolve $\to P$ into two components.
(i) $p cos θ$ along OP
(ii) $p sin θ$ perpendicular to OQ
Now, Point P is on the axial line w.r.t.p $cos θ$
$∴ E_{1} = \frac{2 p cos θ}{4 π ɛ_{0} r^{3}}$ along PD
Point P is on the equatorial line $w . r . t . p sin θ$
$∴ E_{2} = \frac{p sin θ}{4 π ɛ_{0} r^{3}}$ along PC
Since $E_{1} and E_{2}$ are perpendicular to each other, so the resultant electric field is given by,
$E = \sqrt{E_{1}^{2} + E_{2}^{2} + 2 E_{1} E_{2} cos θ}$
$B u t θ = 90^{\circ}$
$∴ E = \sqrt{E_{1}^{2} + E_{2}^{2} + 2 E_{1} E_{2} {cos 90}^{\circ}}$
$E = \sqrt{E_{1}^{2} + E_{2}^{2} + O}$
$E = \sqrt{E_{1}^{2} + E_{2}^{2}}$
$E = \sqrt{{(\frac{2 p cos θ}{4 π ɛ_{0} r^{3}})}^{2} + {(\frac{p sin θ}{4 π ɛ_{0} r^{3}})}^{3}}$
$E = \frac{p}{4 π ɛ_{0} r^{3}} \sqrt{4 {cos}^{2} θ + {sin}^{2} θ}$
$E = \frac{p}{4 π ɛ_{0} r^{3}} \sqrt{3 {cos}^{2} θ + {cos}^{2} θ + {sin}^{2} θ}$
since ${sin}^{2} θ + {cos}^{2} θ = 1$
$∴ E = \frac{p}{4 π ɛ_{0} r^{3}} \sqrt{3 {cos}^{2} θ + 1}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile