Calculate the electric field intensity at point situated at a distance r along the axial line of an electric dipole. What is the electric field when r greater than length of dipole ?

Text Solution

Verified by Experts

Consider an electric dipole consisting of charges + q and -9. The length of dipole is 2 a. Consider a point P at a distance r from the centre of the dipole on the axial line of the dipole.

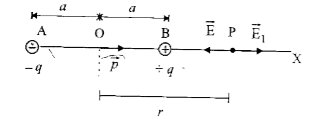
Electric field intensity at P due to + q charge is given by $= \frac{1}{4 π ɛ_{0}} \frac{q}{{(B P)}^{2}} along BP$
${\to E}_{1} = \frac{1}{4 π ɛ_{0}} \frac{q}{{(r - a)}^{2}}, along PA$
Electric field intensity at P due to charge is given by
${\to E}_{2} = \frac{1}{4 π ɛ_{0}} \frac{q}{A P^{2}}, along PA$
$= \frac{1}{4 π ɛ_{0}} \frac{q}{{(r + a)}^{2}} along BP$
Since $∣ ∣ {\to E}_{1} ∣ ∣ > ∣ ∣ {\to E}_{2} ∣ ∣ and {\to E}_{1} and {\to E}_{2}$ are in opposite direction.
$∴ \to E = {\to E}_{1} - {\to E}_{2} along BP$
$= [\frac{1}{4 π ɛ_{0}} \frac{q}{{(r - a)}^{2}} - \frac{1}{4 π ɛ_{0}} \frac{q}{{(r + a)}^{2}}]$
$= \frac{q}{4 π ɛ_{0}} [\frac{1}{{(r - a)}^{2}} - \frac{1}{{(r + a)}^{2}}]$
$= \frac{q}{4 π ɛ_{0}} [\frac{{(r + a)}^{2} - {(r - a)}^{2}}{(r^{2} - a^{2})}]$
$= \frac{q}{4 π ɛ_{0}} [\frac{r^{2} + a^{2} + 2 r a - (r^{2} + a^{2} - 2 r a)}{{(r^{2} - a^{2})}^{2}}]$
=q/(4 pi varepsilon_(0))[(cancelr^(2)+cancela^(2)+2ra-cancelr^(2)-cancela^(2)+2ra))/((r^(2)-a^(2))^(2))]
$\frac{q}{4 π ɛ_{0}} [\frac{4 r a}{{(r^{2} - a^{2})}^{2}}]$
$\frac{q}{4 π ɛ} \frac{2 r \times 2 a}{{(r^{2} - a^{2})}^{2}}$
We know that $q \times 2 a = \to p$ , where p is dipole moment.
$\to E = \frac{2 r \to p}{4 π ɛ_{0} {(r^{2} - a^{2})}^{2}}$
$∴ \to E = \frac{2 r \to p}{4 π ɛ_{0} {(r^{2} - a^{2})}^{2}}$
The direction of the electric field intensity at a point on the axial line is along the (+) X-axis. (along BP)
The magnitude of electric field intensity is given by
$E = \frac{2 r p}{4 π ɛ_{0} {(r^{2} - a^{2})}^{2}} ... (1)$
Special Case
When r > > > a. i.e. Pis at very large distance as compared to ipole length.
$∴ a^{2}$ can be neglected in comparison to $r^{2}$
$∴$ the equation (1) become
$E = \frac{2 r p}{4 π ɛ_{0} {(r^{2} - 0)}^{2}}$
E=(2cancelrp)/(4 pi varepsilon_(0)r^(43))
$E = \frac{2 p}{4 π ɛ_{0} r^{3}}$
$E \propto \frac{1}{r^{3}}$

Updated on:21/07/2023