Derive electric field intensity due to uniformly charged ring or circular loop.

Text Solution

Verified by Experts

Consider a uniformly charged thin ring of radius a. Let $λ$ be the linear charge density of the ring.
Let P be the point on the axis of the ring at a distance r from the centr of the ring.
Consider a small element of length dl on the ring, distant $C P = \sqrt{r^{2} + a^{2}}$ from point P.
Charge on the element.
$d q = λ d l$
$∴$ the electric field intensity due to this small element at point P is,
$d E = \frac{1}{4 π ɛ_{0}} \frac{d q}{C P^{2}}$
Since. $d q = λ d l$
$∴ d E = \frac{1}{4 π ɛ_{0}} \frac{λ d l}{C P^{2}}$

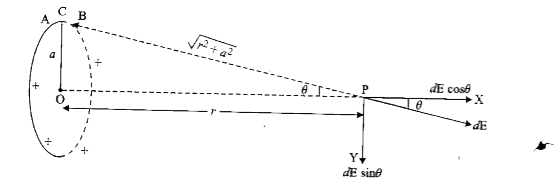
In right angled $Δ A O P, C P^{2} = r^{2} + a^{2}$
$∴ d E = \frac{1}{4 π ɛ_{0}} \frac{λ d l}{(r^{2} + a^{2})} ... (1)$
where dE makes an angle $θ$ with the axis of the ring.
Resolve $d E$ into two component
(i) $d E cos θ$ parallel to the axis of the ring.
(ii) $d E sin θ$ perpendicular to the axis of ring.
Horizontal component $d E cos θ$ are added up because they are in the same direction. $d E sin θ$ component of electric field is cancelled out as they are equal and opposite in direction.
$∴$ the net electric field intensity is
$E = \sum d E cos θ = \int whole ring d E cos θ$
$∴$ from equation (1)
$E = \int whole ring \frac{1}{4 π ɛ_{0}} \frac{λ d l}{(r^{2} + a^{2})} cos θ ... (2)$
From $Δ A O P$
$cos θ = \frac{r}{C P} = \frac{r}{{(r^{2} + a^{2})}^{1 / 2}}$
from eq., (2)
$E = \int wholering d l = circumference of ring = 2 = π a$
$E = \frac{λ r}{4 π ɛ_{0} {(r^{2} + a^{2})}^{3 / 2}} \times 2 π a$
$= \frac{(λ 2 π a) r}{4 π ɛ_{0} {(r^{2} + a^{2})}^{3 / 2}}$
We know that, $λ (2 π a) = q$
$E = \frac{q r}{4 π ɛ_{0} {(r^{2} + a^{2})}^{3 / 2}}$
Direction of electric field intensity due to ring is along the axis the of ring.
(i) When x >>>> a then $r^{2} + a^{2} \approx r^{2}$
$∴ E = \frac{1}{4 π ɛ_{0}} \frac{q r}{{(r^{2})}^{3 / 2}}$
$E = \frac{1}{4 π ɛ_{0}} \frac{q r}{r^{3}}$
$E = \frac{1}{4 π ɛ_{0}} \frac{q r}{r^{2}} along OP$
(ii) When $x = 0$ (i.e., P lies at the center of the ring)
$∴ E = \frac{1}{4 π ɛ_{0}} \frac{0}{r^{2}} = 0$
There is no electric field at the centre of ring.

Updated on:21/07/2023