Add
x2–y2–1,y2–1–x2,1–x2–y2Solution in Punjabi
The correct Answer is:−x2−y2−1
Step by step video, text & image solution for Addx^2 – y^2 – 1, y^2 – 1 – x^2, 1 – x^2 – y^2 by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ALGEBRAIC EXPRESSIONS BOOK - NAND LAL PUBLICATIONCHAPTER - ALGEBRAIC EXPRESSIONS EXERCISE - EXERCISE 12.3
32 Videos
- ALGEBRAIC EXPRESSIONS BOOK - NAND LAL PUBLICATIONCHAPTER - ALGEBRAIC EXPRESSIONS EXERCISE - EXERCISE 12.4
4 Videos
- ALGEBRAIC EXPRESSIONS BOOK - NAND LAL PUBLICATIONCHAPTER - ALGEBRAIC EXPRESSIONS EXERCISE - EXERCISE 12.1
60 Videos
- EXPONENTS AND POWERS BOOK - NAND LAL PUBLICATIONCHAPTER - EXPONENTS AND POWERS EXERCISE - SAMPLE PAPER FOR PRACTICE
8 Videos
Similar Questions
If m = 2, find the value of:
m – 2
View SolutionObserve the patterns of digits made form line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.
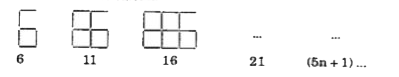
How many segments are required to from 5, 10, 100 digits of the kind 6, 4, 8?
View SolutionGet the algebraic expressions in the following cases using variables, constants and arithmetic operations
.Subtraction of z from y.
View SolutionMatch the following

View SolutionIf 2x+2y=2x+y, then dydx is equal to −2y2x (b) 11−2x 1−2y (d) 2x(1−2y)2y(2x−1)
View SolutionEquation of a line which is tangent to both the curve y=x2+1 and y=x2 is y=√2x+12 (b) y=√2x−12 y=−√2x+12 (d) y=−√2x−12
View SolutionProve that : tan(12){sin−1(2x1+x2)+cos−1(1−y21+y2)}=x+y1−xy , if |x|<1, y>0 and xy<1 .
View Solution(x+2)(x+1)=(x−2)(x−3)
(y+3)(y+2)=(y−1)(y−2)
View Solutionयदि y=(sin−1x)2 हो, तो सिद्ध कीजिये कि -
(1−x2)y2−xy1−2=0
View Solution∣∣ ∣ ∣ ∣ ∣ ∣∣(x+1x)2(x−1x)21(y+1y)2(y−1y)21(z+1z)2(z−1z)21∣∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionThe factors of x3−1+y3+3xy are
(a) (x−1+y)(x2+1+y2+x+y−xy)
(b)(x+y+1)(x2+y2+1−xy−x−y)
(c)(x−1+y)(x2−1−y2+x+y+xy)
(d)3(x+y−1)(x2+y2−1)
View Solutionਜੋੜੋ:- x2−y2−1,y2−1−x2,1−x2−y2
View Solutionसरल कीजिए
1+y(1−x)(1−y2)+x2(y+x)(1−x)(y2−x2)−y2(y+1)(y2−1)(x−y)
View SolutionThe locus of the middle point of the chord of the circle x2+y2=a2 such that the chords passes through a given point (x1,y1), is :
a)x2+y2−xx1−yy1=0 b)x2+y2=x21+y21 c)x+y=x2+y1 d)x+y=x21+y21
View Solutionजोड़िए :
x2−y2−1,y2−1−x2,1−x2−y2
View SolutionAdd
x2–y2–1,y2–1–x2,1–x2–y2
View Solution
