Take a cut-out a parallelogram, say, ABCD (see figure). Let its diagonals ¯¯¯¯¯¯ACand¯¯¯¯¯¯DB meet at O.
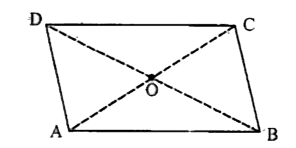
Find the mid-point of ¯¯¯¯¯¯AC by a fold, placing C on A. Is the mid-point same as O?
Does this show that diagonal ¯¯¯¯¯¯DB bisects the diagonal ¯¯¯¯¯¯AC at the point O ? Discuss it with your friends. Repeat the activity to find where the mid-point of ¯¯¯¯¯¯DB could lie.
Text Solution
The correct Answer is:the diagonals of a parallelogram bisect each other.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - SWAN PUBLICATIONCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - THINK, DlSCUSS AND WRITE4videos
UNDERSTANDING QUADRILATERALS
- BOOK - SWAN PUBLICATIONCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - QUESTION1videos
UNDERSTANDING QUADRILATERALS
- BOOK - SWAN PUBLICATIONCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - TRY THESE12videos
UNDERSTANDING QUADRILATERALS
- BOOK - SWAN PUBLICATIONCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - Exercise 6.437videos
SQUARES AND SQUARE ROOTS
- BOOK - SWAN PUBLICATIONCHAPTER - VISUALISING SOLID SHAPES EXERCISE - Exercise 10.311videos
VISUALISING SOLID SHAPES
Similar Questions
. Knowledge Check
- Question 1 - Select One
E and F are mid-points of diagonals AC and BD of □ABCD. If G is the mid-point of seg EF, then
A4 ¯¯¯¯¯¯AGB¯0C0D2¯¯¯¯¯¯GC - Question 2 - Select One
If diagonals of a parallelogram ABCD intersect each other in M, then ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC+¯¯¯¯¯¯OD =
A¯¯¯¯¯¯¯OMB2¯¯¯¯¯¯¯OMC3¯¯¯¯¯¯¯OMD4¯¯¯¯¯¯¯OM - Question 3 - Select One
Let PQRS be a parallelogram whose diagonals PR and QS intersect at O'. IF O is the origin then : ¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR+¯¯¯¯¯¯OS=
A4 ¯¯¯¯¯¯¯¯OO'B3 ¯¯¯¯¯¯¯¯OO'C2 ¯¯¯¯¯¯¯¯OO'D¯¯¯¯¯¯¯¯OO'
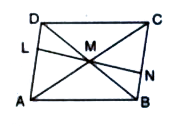
Given Parallelogram ABCD in which diagonals AC and BD at M.Prove M is mid-point of LN.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View SolutionABCD is a parallelogram. L and M are respectively mid points of sides AB and DC. Prove that LD and MB trisects diagonals AC.
View SolutionIf D is the mid -point of side AB of ΔABC, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AC=
View Solution