Using the SONAR, sound pulses are emitted at the surface of water. These pulses after being reflected from the surface of water bottom are detected. If the time interval from the emission to the detection of the sound pulses is 2 seconds, find the depth of the water.
Speed of sound waves in water, v = 1498 m/s
Total time from emission to detection, t=2 seconds
Let depth of water = d
Total distance travelled by sound pulses =
Now, distance = velocity time
or
i.e. depth of water = 1498 m
Similar Questions
A sonar emits pulses on the surface of water which are detected after reflection from its bottom at a depth of 1531m. If the time interval between the emission and detection of the pulse is 2s, find the speed of sound in water.
View SolutionA pulse shown here is reflected from the rigid wall A and then from free end B. The shape of the string after these 2 reflection will be
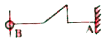
View Solution
Knowledge Check
A sonar device fixed to the ship is used to find the depth of the ocean. The ultrasonic sound produced gets reflected from the ocean bed and the time taken for the reflected sound to reach the sonar is 4 s, then write the following steps in sequence to find the depth of the ocean bed (d). (Speed of sound in ocean water is 1500 m s−1)
(A) Use the formula, speed = distance travelled by the sound (2d)Total time taken (t)
(B ) The distance travelled by the sound is equal to twice the depth of the ocean bed (d).
(C )Note the total time (1) taken by the reflected sound to reach the sonar from ocean bed from given data.
(D ) Substitute the values in the given formula, and find the value of 'd'.Aa b c dBb a c dCd a c bDc b a dWrite the following statements in a sequential order to find the depth of the ocean bed by the using sonar .
(A) The depth of the ocean bed can be found by d = vt2.
(B) At the bottom of a ship two devices , one is transmitter which products ultrasonics and a receiver for the detection of the reflected ultrasonics from the ocean bed are fixed .
(C) The velocity fo ultrasonics in ocean water is 'v' and the time taken to receive the reflected ultrasonics from the ocean bed be 'f'.
(D) If the depth of ocean bed is 'd' , then v=d+dt=2dt.Aa b c dBb a c dCd a c bDc b a d
A pulse shown here is reflected from the rigid wall A and then from free end B. The shape of the string after these 2 Reflection will be.
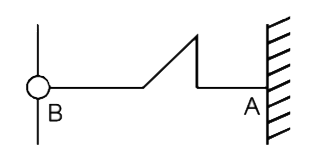
View SolutionA sonar deivce attached to a ship sends. Ultrasomic waves in the sea. These waves are reflected from the bottom of the sea. If the ultrasonic waves take 4 seconds to travel from the ship to the bottom of the sea and back to the ship (in the form of an echol), what is the depth of the sea? (Speed of sound in water =1500m/s).
View SolutionIn a SONAR, ultrasonic waves are sent into the sea water and the reflected waves from a sunken ship are received after 2.0 s. If the velocity of waves in sea water is 1450 m s−1 , find the depth of the sunken ship.
View SolutionA message was transmitted from boat which returned to the sender after reflection from the bottom of the sea in 0.8 s. If the velocity of sound in water is 1500ms−1 then find the depth of sea.
View SolutionA ship on the surface of water sends a signal and receives it back from a submarine inside water after 4 s. Calculate the distance of the submarine from the ship. (The speed of sound in water is 1450 m s−1).
View SolutionA ship on the surface of water sends a signal and receives it back after 4 s from a submarine inside the water. Calculate the distance of the submarine from the ship. [The speed of sound in water is 1450 m s−1]
View Solution
