The area enclosed by the curves y=sinx+cosx and y=|cosx−sinx| over the interval [0,π/2] is
A
4(√2−1)
B
2√2(√2−1)
C
2(√2+1)
D
2√2(√2+1)
Text Solution
The correct Answer is:B
|
Similar Questions
Knowledge Check
The area enclosed by the curvesy=sinx+cosxandy=|cosx−sinx| over the interval [0,π2]
A4(√2−1)B2√2(√2−1)C2(√2+1)D2√2(√2+1)The area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and x=3π2, is
A(4√2−2) sq unitsB(4√2+2) sq unitsC(4√2−1) sq unitsD(4√2+1) sq unitsThe angle at which the curves y=sinx and y=cosx intersect in [0,π], is
A±tan−1√2B±tan−12√2C±tan−11√2Dnone of these
Area enclosed by the curves y=sinx+cosxandy=|cosx−sinx| and the lines x=0andx=π2
View SolutionThe angle between the curves y=sinx and y=cosx is
View SolutionThe area bounded by the curves y=cosx and y=sinx between the ordinates x=0 and x=3π2 is
View Solution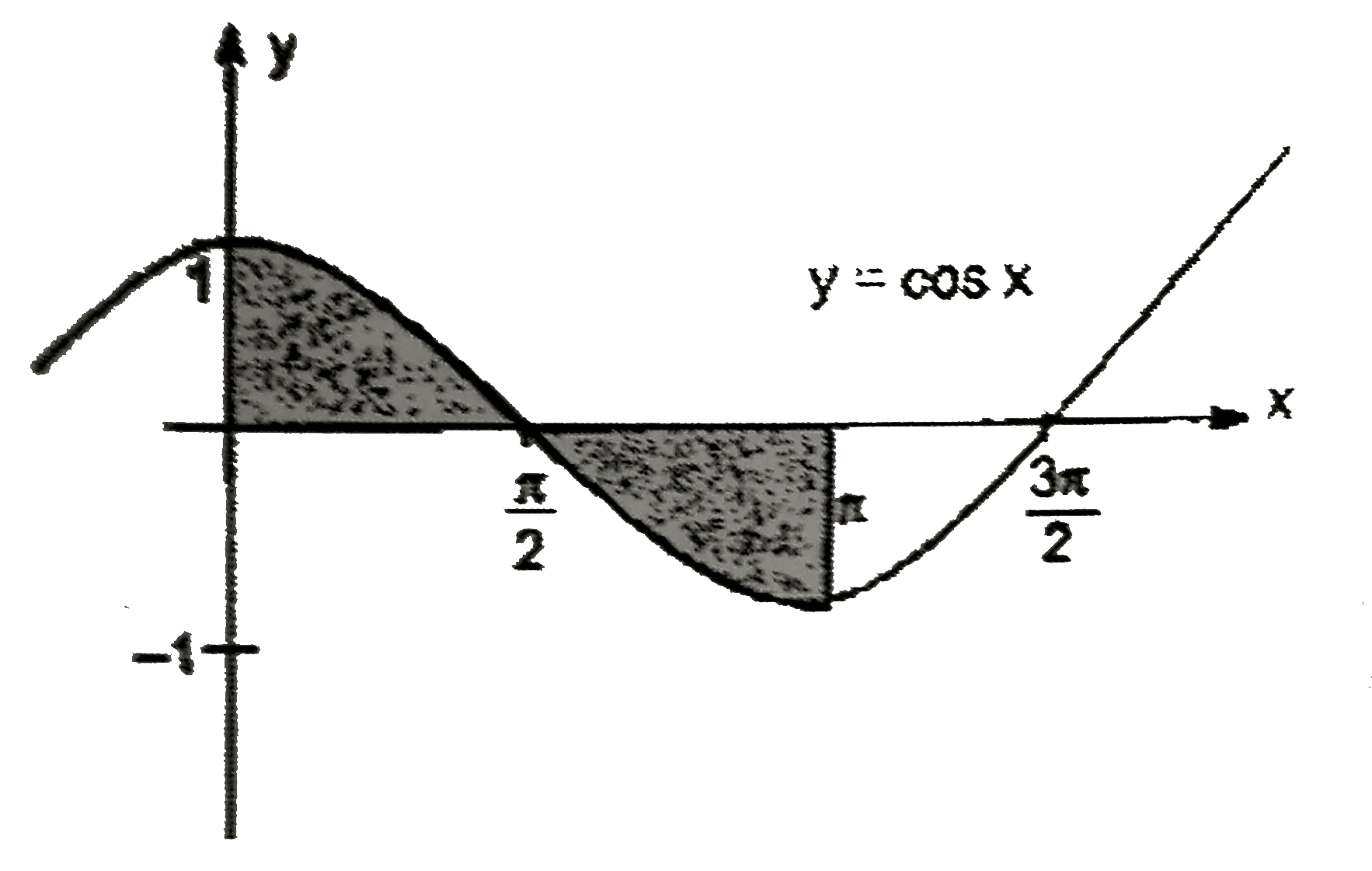
(a). Find the area under the curve y=cosx over the interval [0,π/2] and [0,π]
View SolutionThe area of the region bounded by the curves y=√1+sinxcosx and y=√1−sinxcosx bounded by the lines x=0 and x=π4 is
View Solution
