A thin uniform wire AB of unknown resistance is connected between points A and B. AP and QR are thick conducting stripes. A battery of unknown emf e and a galvanometer (with a sliding jockey connected to it) are available. Connections are to be made to find emf c, resistance of wire AB and length of AB.,The battery with galvanometer is connected between points A and B in two alternative way such that j ockey when passed on wire AB at distance 80 cm and 120 cm respectively from end A, galvanometer shows no deflection.
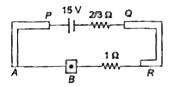
If one end of battery with galvanometer is connected to point R and jockey is pressed on AB at distance 180 cm from end A, the deflection in galvanometer is zero then find:
The emf of battery is ε=
2V
5 V
4 V
10 V
The correct Answer is:C
Put R=103 in equation (i)
We get ε=1553+103×3200×8=3×163×25,ε=4V
Similar Questions
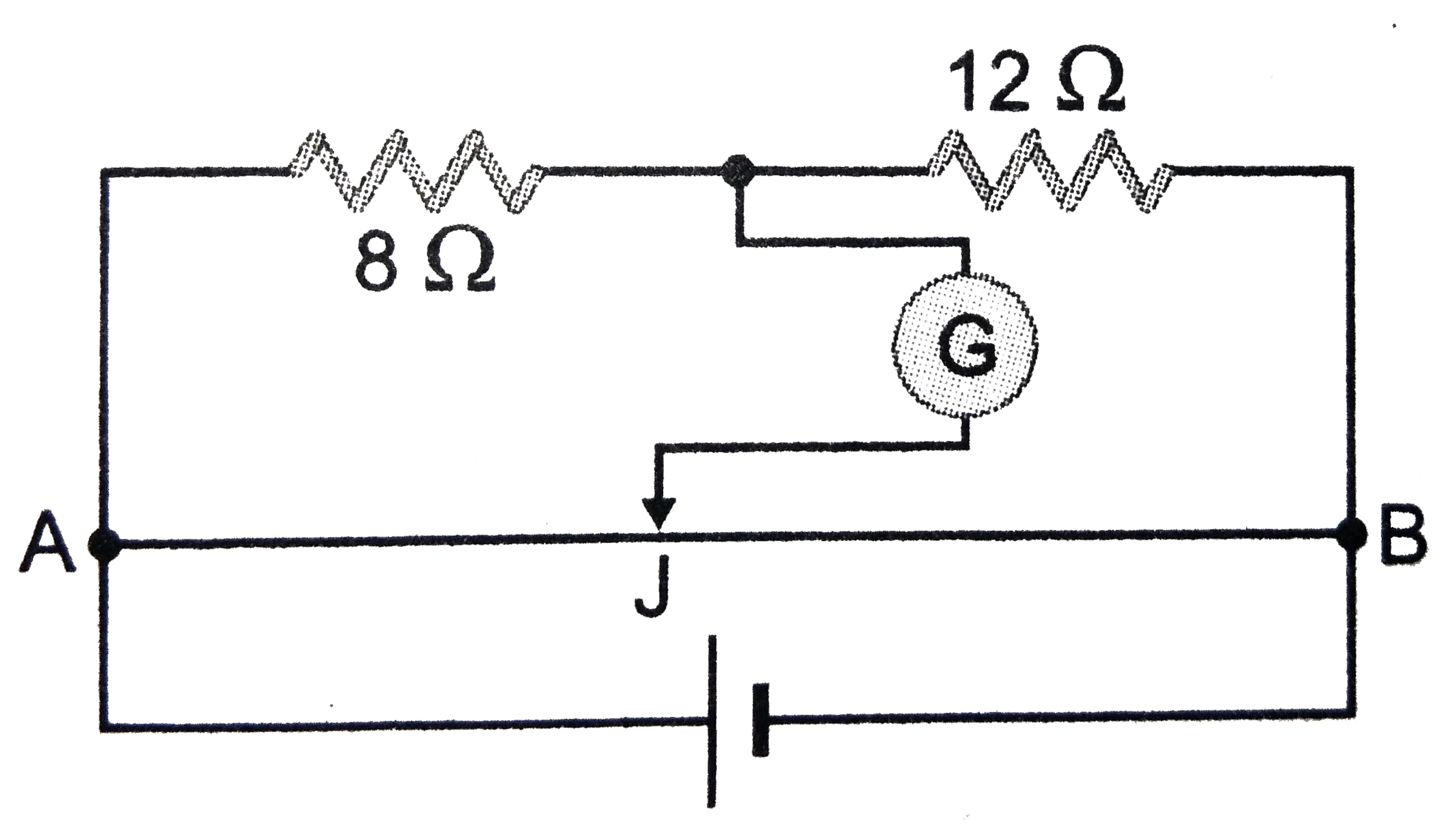
A thin uniform wire Ab of length 1m, an unknown resistance X and a resistance of 12Ω are connected by thick conducting strips, as shown in the figure. A battery and a galvanometer (with a sliding jockey connected to it) are also available. Connections are to be made to measure the unknown resistance X using the principle of Wheatstone bridge. Answer the following questions.
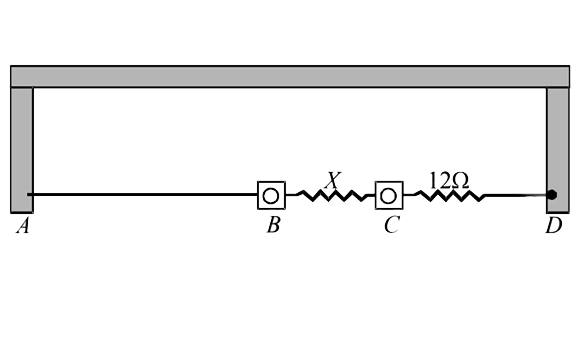
(a) Are there positive and negative terminals on the galvanometer?
(b) Copy the figure in your answer book and show the battery and the galvanometer (with jockey) connected at appropriate points.
View SolutionA thin uniform wire AB of length 1m, an unknown resistance X and a resistance of 12Ω are connected by thick conducting strips, as shown in the figure. A battery and a galvanometer (with a sliding jockey connected to it) are also available. Connections are to be made to measure the unknown resistance X. Using the principle of Wheatstone bridge answer the following questions :
(a) Are there positive and negative terminals on the galvanometer?
(b) Copy the figure in your answer book and show the battery and the galvanometer (with jockey connect at appropriate points.
(c) After appropriate connections are made, it is found that no deflection takes place in th, from galvanometer when the sliding jockey touches the wire at a distance of 60cm from A. Obtain value of the resistance X.
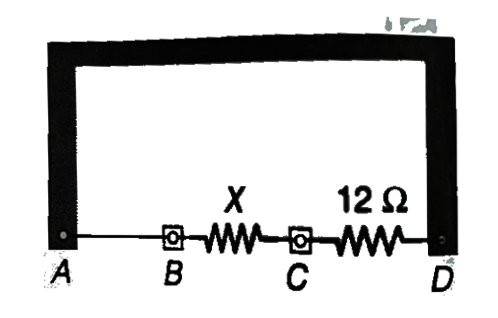
View SolutionA thin uniform wire AB of length 1m, an unknown resistance X and a resistance of 12Ω are connected by thick conducting strips, as shown in the figure. A battery and a galvanometer (with a sliding jockey connected to it) are also available. Connections are to be made to measure the unknown resistance X. Using the principle of Wheatstone bridge answer the following questions :
(a) Are there positive and negative terminals on the galvanometer?
(b) Copy the figure in your answer book and show the battery and the galvanometer (with jockey connect at appropriate points.
(c) After appropriate connections are made, it is found that no deflection takes place in th, from galvanometer when the sliding jockey touches the wire at a distance of 60cm from A. Obtain value of the resistance X.

View SolutionA thin uniform wire AB of length 1m, an unknown resistance X and a resistance of 12Ω are connected by thick conducting strips, as shown in the figure. A battery and a galvanometer (with a sliding jockey connected to it) are also available. Connections are to be made to measure the unknown resistance X. Using the principle of Wheatstone bridge answer the following questions :
(a) Are there positive and negative terminals on the galvanometer?
(b) Copy the figure in your answer book and show the battery and the galvanometer (with jockey connect at appropriate points.
(c) After appropriate connections are made, it is found that no deflection takes place in th, from galvanometer when the sliding jockey touches the wire at a distance of 60cm from A. Obtain value of the resistance X.

View SolutionA thin uniform wire AB of length 1m, an unknown resistance X and a resistance of 12Ω are connected by thick conducting strips, as shown in the figure. A battery and a galvanometer (with a sliding jockey connected to it) area also available. Connections are to be made to measure the unknown resistance X using the principle of Wheatstone bridge. Answer the following questions.

(a) Are there positive and negative terminals on the galvanometer ?
(b) Copy the figure in your answer book and show the battery and the galvanometer (with jockey) connected at apalphariate points.
( c) After apalphariate connections are made, it is found that no deflection takes place in the galvanometer when the sliding jockey touches the wire at a distance of 60cm from A. Obtain the value of the resistance X.
View SolutionA thin uniform wire AB of length 1m, an unknown resistance X and a resistance of 12Ω are connected by thick conducting strips, as shown in the figure. A battery and a galvanometer (with a sliding jockey connected to it) are also available. Connections are to be made to measure the unknown resistance X. Using the principle of Wheatstone bridge answer the following questions :
(a) Are there positive and negative terminals on the galvanometer?
(b) Copy the figure in your answer book and show the battery and the galvanometer (with jockey connect at appropriate points.
(c) After appropriate connections are made, it is found that no deflection takes place in th, from galvanometer when the sliding jockey touches the wire at a distance of 60cm from A. Obtain value of the resistance X.

View SolutionWhat is the change in experiment if battery is connected between B and D and galvanometer is connected across A and C ?
View SolutionA uniform wire AB of length 1 m, an unknown resistance X and a resistance of 12Ω are connected to a battery and a galvanometer G as shown in the figure. The galvanometer shows no deflection when AJ=60 cm. What is the value of X (in ohm) ?
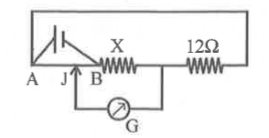
View SolutionThe wire AB of slide wire bridge 68 is 400 cm long. Where should the jockey J whose one end connected to galvanometer,the other end can be connected to AB, so that galvanometer shows no deflection ?
View SolutionA secondary cell of emf 2 V and finternal resistance 0.1 Ω is connected to the ends of a uniform wire of length 1 m and resistacne 12 Ω.A primary cell of emf 1.5 V in series with a galvancometer is connected to two points on the wire. If the galvanometer shows no deflection find the distance between the points.
View Solution
